Дослідження поведінки шаруватого розширення вдосконаленого композитного ламінату, армованого вуглецевим волокном

МЕХАНІКА ТА ІНЖЕНЕРІЯ - Чисельні обчислення та аналіз даних
Механіка та інженерія — Чисельні розрахунки та аналіз даних 2019. Академічна конференція, 19-21 квітня 2019 р., Пекін
19-21 квітня 2019 року, Пекін, Китай

Дослідження поведінки шаруватого розширення вдосконаленого композитного ламінату, армованого вуглецевим волокном

Гун Ю^1*Ван Яна², Пен Лей³, Чжао Лібінь⁴, Чжан Цзянюй¹

¹Чунцінський університет, Чунцін, 400044, Китай
²Китайський авіаційний науково-дослідний інститут, Пекінський науково-дослідний інститут аеронавігаційних матеріалів, Пекін, 100095, Китай
³Китайські комерційні літаки Пекінський дослідницький центр технологій цивільної авіації, Пекін, 102211, Китай
⁴Пекінський університет аеронавтики та астронавтики, Пекін, 100191, Китай

АнотаціяШарувата структура є однією з найпоширеніших конфігурацій композитів, але розшарування стає її основним способом руйнування через слабкі міжшарові властивості. Дослідження поведінки багатошарового ламінату при розшаруванні та розширенні, що зазвичай використовується в інженерній практиці, завжди було гарячою темою для науковців. У цій статті представлені результати дослідження розшарування композитів, армованих вуглецевим волокном, у Чунцінському університеті та Лабораторії втомного руйнування Пекінського університету аеронавтики та астронавтики, з двох аспектів: експериментального дослідження та числового моделювання. Нарешті, запропоновано напрямок розвитку цієї галузі.

Ключові слова:вуглецево-армований композит, ламінат, розшарування, втомна стратифікація

вступ

Композитні матеріали мають чудові властивості, такі як висока питома міцність та висока питома жорсткість, і широко використовуються в аерокосмічній галузі, енергетичних технологіях, цивільному транспорті та будівництві. Під час обробки та використання композитних матеріалів волокна та матриця зазнають різного ступеня пошкодження під навантаженням. Поширені режими руйнування композитних ламінатів включають міжшарове пошкодження та пошкодження всередині шарів. Через відсутність армування в напрямку товщини, поперечні механічні властивості ламінату погані, і пошкодження відшаровуванням дуже ймовірне під впливом зовнішніх ударних навантажень. Виникнення та розширення шаруватих пошкоджень призведе до зниження жорсткості та міцності конструкції, а також спричинить катастрофічні аварії.^[1-3]Таким чином, проблема розшарування все більше і більше стосується структурного проектування та аналізу міцності композитних матеріалів, і необхідно вивчати поведінку шаруватого розширення композитних матеріалів.^[4].

Дослідження поведінки шаруватого розширення ламінату
1. Експериментальне дослідження

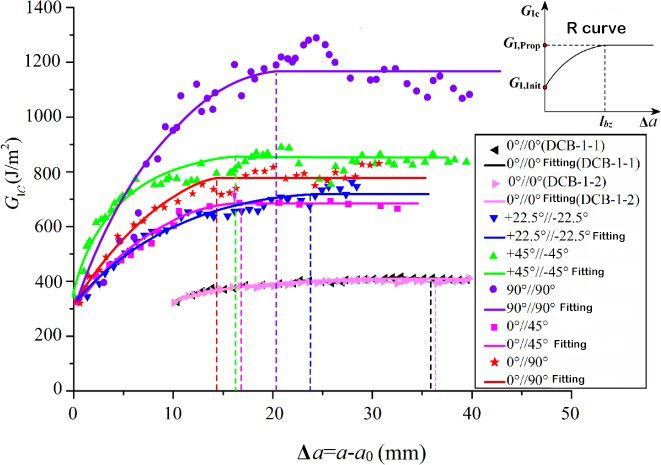
Міжшарова в'язкість руйнування є характерним параметром механічних властивостей між композитними шарами. Відповідні стандарти випробувань були встановлені для визначення міжшарової в'язкості руйнування однонаправлених ламінатів типу I, типу II та I/II. Відповідний випробувальний апарат показано на рисунку 1. Однак багатонаправлені ламінати з композитних матеріалів часто використовуються в реальних інженерних конструкціях. Тому експериментальне дослідження поведінки розшарування та розширення багатонаправлених ламінатів має важливіше теоретичне значення та інженерну цінність. Зародження та розширення шарів багатошарового ламінату відбувається між межами розділу з довільними кутами нашарування, і поведінка шаруватого розширення суттєво відрізняється від поведінки однонаправлених ламінатів, а механізм розширення є складнішим. Дослідники мають відносно мало експериментальних досліджень багатонаправлених ламінатів, і визначення міжшарової в'язкості руйнування ще не встановило міжнародного стандарту. Дослідницька група використовувала вуглецеве волокно T700 та T800 для розробки різноманітних композитних ламінатів з різними кутами накладання межі розділу та вивчала вплив кута накладання межі розділу та перемикання волокон на статичну поведінку та поведінку розшарування втоми. Було виявлено, що волокнисті містки, утворені заднім краєм шару, мають великий вплив на міжшарову в'язкість розтріскування. У міру розширення шару міжшарова в'язкість розтріскування поступово зростає з нижчого початкового значення, і коли шар досягає певної довжини, вона досягає стабільного значення, тобто явища кривої опору R. Початкова в'язкість розтріскування проміжного шару майже дорівнює та приблизно дорівнює в'язкості розтріскування смоли, яка залежить від в'язкості розтріскування самої матриці.^{[5, 6]}Однак значення подовження міжшарової в'язкості руйнування різних інтерфейсів значно відрізняються. Представлено значну залежність від кута нахилу інтерфейсного шару. У відповідь на цю залежність, Чжао та ін.^[5]Виходячи з фізичного механізму джерела стратифікованого опору, вважається, що значення стійкості до міжшарової в'язкості руйнування складається з двох частин, одна частина - це робота руйнування непов'язаного шару розділу, а інша частина - внутрішньошарове пошкодження та волокно. Робота руйнування, спричинена перемиканням. За допомогою аналізу методом скінченних елементів поля фронту напружень шаруватого фронту виявлено, що друга частина роботи руйнування залежить від глибини зони пошкодження фронту розшарування (як показано на рисунку 3), а глибина зони пошкодження пропорційна куту нахилу розділу. Представлено теоретичну модель значення стійкості до в'язкості руйнування I-типу, виражену синусоїдальною функцією кута нахилу розділу.
Гонг та ін.^[7]провели випробування на гібридну стратифікацію I/II за різних співвідношень змішування та виявили, що гібридна стратифікація I/II у ламінаті також має значні характеристики кривої опору R. Завдяки аналізу в'язкості руйнування між різними випробуваними зразками було виявлено, що початкове значення та стабільне значення міжшарової в'язкості руйнування випробуваного зразка значно зростають зі збільшенням співвідношення змішування. Крім того, початкову та стабільну в'язкість руйнування проміжного шару за різних співвідношень змішування можна описати критерієм BK.
Щодо втомної стратифікації, під час випробування також спостерігалося значне утворення містків у волокнах. Аналіз даних випробувань показав, що на розширення композитного матеріалу внаслідок втомної розшаровування впливає «крива опору», тому традиційна модель швидкості розширення втомної стратифікації та порогове значення більше не застосовуються. На основі теоретичного аналізу Чжан та Пен^[4,8,9]ввели опір розширенню від втоми при розшаровуванні, щоб виразити енергію, необхідну для розширення композитних матеріалів від втоми при розшаровуванні, а також запропонували нормалізовану енергію деформації. Швидкість вивільнення - це модель швидкості стратифікованого розширення від втоми та порогове значення контрольних параметрів. Застосовність моделі та нормалізованого порогового параметра підтверджена експериментами. Крім того, Zhao та ін.^[3]всебічно розглянули вплив перемикання волокон, коефіцієнта напружень та коефіцієнта змішування навантаження на поведінку стратифікації втоми та розширення, а також створили нормалізовану модель швидкості стратифікованого розширення втоми з урахуванням впливу коефіцієнта напружень. Точність моделі була перевірена за допомогою випробувань на стратифікацію втоми з різними коефіцієнтами напружень та коефіцієнтами змішування. Для фізичної величини опору стратифікованому розширенню втоми в нормалізованій моделі швидкості стратифікованого розширення втоми, Гонг та ін.^[1]Подолати недоліки методу розрахунку, який може отримати лише обмежену кількість дискретних точок даних за допомогою експериментів, та встановити втому з енергетичної точки зору. Аналітична модель для розрахунку стратифікованого розширеного опору. Модель може реалізувати кількісне визначення стратифікації втоми та опору розширенню, а також забезпечити теоретичну підтримку для застосування запропонованої нормалізованої моделі швидкості стратифікованого розширення втоми.

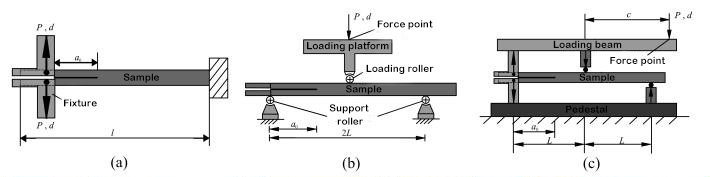Рисунок 1. Схема стратифікованого тестового пристрою

Рисунок 2. Крива опору міжшаровій в'язкості руйнування R^[5]


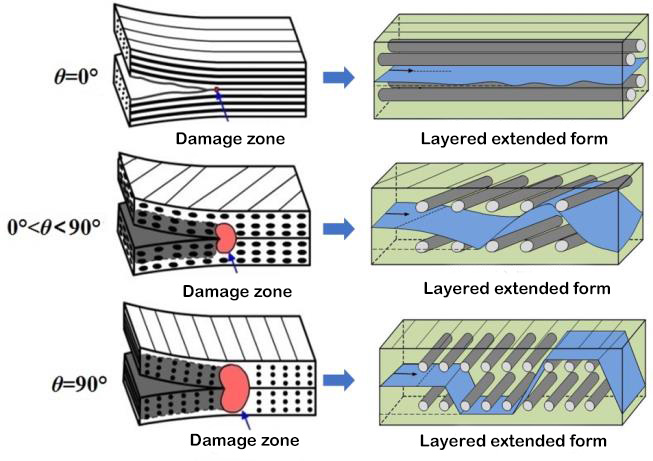
Рисунок 3. Зона пошкодження шаруватої передньої кромки та стратифікована протяжна морфологія^[5]

2. Дослідження чисельного моделювання

Чисельне моделювання шаруватого розширення є важливим змістом досліджень у галузі проектування композитних конструкцій. При прогнозуванні розшаровувального руйнування композитних односпрямованих ламінатів існуючі критерії шаруватого розширення зазвичай використовують постійну міжшарову в'язкість руйнування як основний параметр експлуатаційних характеристик.^[10], шляхом порівняння швидкості вивільнення енергії вершини тріщини та міжшарової в'язкості руйнування. Розмір для визначення розширення нашарування. Механізм руйнування багатонаправлених ламінатів є складним^[11,12], що характеризується значними кривими опору R^[5,13]Існуючі критерії шаруватого розширення не враховують цю особливість і не застосовуються до моделювання поведінки розшарування багатонаправлених ламінатів, що містять волокна. Гонг та ін.^{[10, 13]}удосконалив існуючі критерії стратифікованого розширення та запропонував ввести до критеріїв криву опору R, і на основі цього встановив критерій стратифікованого розширення з урахуванням впливу волоконних містків. Визначення та параметри використання білінійної конститутивної когезійної одиниці систематично досліджувалися числовими методами, включаючи початкову жорсткість інтерфейсу, міцність інтерфейсу, коефіцієнт в'язкості та мінімальну кількість елементів у зоні когезійної сили. Була встановлена ​​відповідна модель параметрів когезійної одиниці. Нарешті, ефективність та застосовність удосконаленого критерію шаруватого розширення та моделі параметрів когезійної одиниці перевіряються за допомогою статичної стратифікаційної перевірки. Однак удосконалені критерії можуть бути використані лише для одновимірних шаруватих симуляцій через позиційні залежності, а не для дво- або тривимірних ієрархічних розширень. Щоб вирішити цю проблему, автор також запропонував нову трилінійну конститутивну когезійну силу з урахуванням волоконних містків.^[14]Конститутивний зв'язок відповідає складному процесу шаруватого розширення з мікроскопічної точки зору та має переваги простих параметрів та чіткого фізичного сенсу.
Крім того, для точного моделювання явища стратифікованої міграції, поширеного в процесі стратифікації багатонаправлених ламінатів^[11,12], Чжао та ін.^[11,12]запропоновано модель наведення траєкторії тріщини на основі розширеного методу скінченних елементів, що імітує спеціальну конструкцію. Ієрархічна міграція в тесті композитної стратифікації. Водночас запропоновано модель шаруватого розширення для зигзагоподібної поведінки шаруватого розширення вздовж шаруватого інтерфейсу 90°/90°, яка точно імітує поведінку шаруватого розширення інтерфейсу 90°/90°.

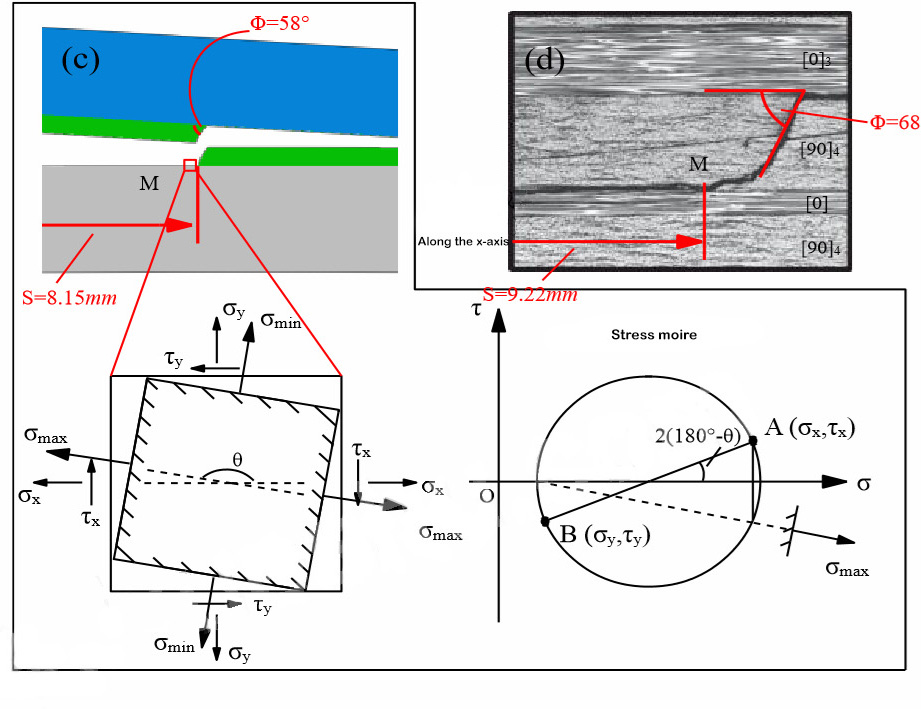Рисунок 4 Чисельне моделювання шаруватої міграції та експериментальні результати^[15]

Висновок

Ця стаття зосереджена на результатах досліджень цієї групи в галузі розшарування композитних шаруватих матеріалів. Експериментальні аспекти включають головним чином вплив кута укладання межі розділу та перемичок волокон на статичну поведінку розширення та розшарування від втоми. Завдяки великій кількості експериментальних досліджень було виявлено, що механізм руйнування багатонаправлених шаруватих матеріалів у композитних матеріалах є складним. Перемички волокон є поширеним механізмом зміцнення багатонаправлених шаруватих матеріалів, що є основною причиною кривої опору R міжшарової в'язкості руйнування. Наразі дослідження кривої опору R при II стратифікації є відносно недостатнім і потребує подальших досліджень. Починаючи з механізму руйнування, запропоновано модель стратифікації втоми, що включає різні фактори впливу, що є напрямком дослідження стратифікації втоми. З точки зору числового моделювання, дослідницька група запропонувала покращений критерій ієрархічного розширення та когезивну конститутивну модель для врахування впливу перемичок волокон на поведінку стратифікованого розширення. Крім того, для кращого моделювання явища ієрархічної міграції використовується розширений метод скінченних елементів. Цей метод усуває необхідність дрібного поділу комірок, усуваючи проблеми, пов'язані з повторним поділом сітки. Він має унікальні переваги в моделюванні стратифікації довільних форм, і в майбутньому потрібні додаткові інженерні прикладні дослідження цього методу.^[16].

Посилання

[1] Y Gong, L Zhao, J Zhang, N Hu. Нова модель для визначення опору втомному розшаруванню в композитних ламінатах з точки зору енергії. Compos Sci Technol 2018; 167: 489-96.
[2] Л. Чжао, І. Ван, Дж. Чжан, І. Гун, Н. Ху, Н. Лі. Модель на основі XFEM для моделювання зигзагоподібного розшарування в шаруватих композитах під дією навантаження режиму I. Compos Struct 2017; 160: 1155-62.
[3] Л. Чжао, І. Гун, Дж. Чжан, І. Ван, З. Лу, Л. Пен, Н. Ху. Нова інтерпретація поведінки росту втомного розшарування в багатонаправлених ламінатах з вуглецевого волокна. Compos Sci Technol 2016; 133: 79-88.
[4] Л. Пенг, Дж. Чжан, Л. Чжао, Р. Бао, Х. Ян, Б. Фей. Ріст розшарування в режимі I багатонаправлених композитних ламінатів під навантаженням від втоми. J Compos Mater 2011; 45: 1077-90.
[5] Л. Чжао, І. Ван, Дж. Чжан, І. Гун, З. Лу, Н. Ху, Дж. Сюй. Модель платоподібної тріщиностійкості в багатонаправлених ламінатах з вуглецевого волокна, що залежить від інтерфейсу, під час навантаження режиму I. Композити, частина B: Інженерія 2017; 131: 196-208.
[6] Л. Чжао, І. Гун, Дж. Чжан, І. Чен, Б. Фей. Моделювання зростання розшаровування в багатонаправлених ламінатах під дією навантажень режиму I та змішаного режиму I/II з використанням когезійних елементів. Compos Struct 2014; 116: 509-22.
[7] Y Gong, B Zhang, L Zhao, J Zhang, N Hu, C Zhang. Поведінка R-кривої змішаного режиму розшарування I/II у вуглецевих/епоксидних ламінатах з однонаправленими та багатонаправленими інтерфейсами. Compos Struct 2019. (На рецензуванні).
[8] Л. Пен, Дж. Сюй, Дж. Чжан, Л. Чжао. Змішаний режим розшарування багатонаправлених композитних ламінатів під навантаженням від втоми. Eng Fract Mech 2012; 96: 676-86.
[9] Дж. Чжан, Л. Пенг, Л. Чжао, Б. Фей. Швидкості зростання та пороги втомного розшарування композитних ламінатів при змішаному навантаженні. Int J Fatigue 2012; 40: 7-15.
[10] Y Gong, L Zhao, J Zhang, Y Wang, N Hu. Критерій поширення розшарування, включаючи вплив утворення волоконних містків для змішаного I/II розшарування в багатонаправлених ламінатах з вуглецевого волокна. Compos Sci Technol 2017; 151: 302-9.
[11] Y Gong, B Zhang, SR Hallett. Міграція розшарування в багатонаправлених композитних ламінатах під дією квазістатичного та втомного навантаження режиму I. Compos Struct 2018; 189: 160-76.
[12] Y Gong, B Zhang, S Mukhopadhyay, SR Hallett. Експериментальне дослідження міграції розшарування в багатонаправлених ламінатах під час статичного та втомного навантаження в режимі II у порівнянні з режимом I. Compos Struct 2018; 201: 683-98.
[13] Y Gong, L Zhao, J Zhang, N Hu. Удосконалений критерій степеневого закону для поширення розшарування з урахуванням великомасштабного перекриття волокон у композитних багатонаправлених ламінатах. Compos Struct 2018; 184: 961-8.
[14] Y Gong, Y Hou, L Zhao, W Li, G Yang, J Zhang, N Hu. Нова трилінійна когезійна зона для зростання розшарування в ламінатах DCB з ефектом перетину волокон. Compos Struct 2019. (Ще буде подано)
[15] Л. Чжао, Дж. Чжі, Дж. Чжан, З. Лю, Н. Ху. Моделювання розшарування в композитних ламінатах за допомогою рентгенівських скінченних електронів. Композити, частина А: Прикладна наука та виробництво, 2016; 80: 61-71.
[16] Чжао Лібінь, Гун Юй, Чжан Цзяньюй. Прогрес досліджень поведінки стратифікованого розширення волокнисто-армованих композитних ламінатів. Журнал аеронавтичних наук 2019: 1-28.

Джерело:Гун Юй, Ван Яна, Пен Лей, Чжао Лібінь, Чжан Цзяньюй. Дослідження поведінки стратифікованого розширення вдосконалених композитних ламінатів, армованих вуглецевим волокном [C]. Механіка та інженерія - Чисельні обчислення та аналіз даних 2019. Академічна конференція. Китайське товариство механіків, Пекінське товариство механіків, 2019. через Іксуешу