力学と工学 - 数値計算とデータ分析
力学と工学 - 数値計算とデータ分析 2019 学術会議、2019年4月19日~21日、北京
2019年4月19日~21日、中国北京
先進炭素繊維強化複合材料積層板の層状膨張挙動に関する研究
コン・ユ1*、王ヤナ2、彭磊3、趙立彬4、張建宇1
1重慶大学、重慶市、400044、中国
2中国航空研究所 北京航空材料研究所、北京、100095、中国
3中国商用航空機北京民間航空機技術研究センター、北京、102211、中国
4北京航空航天大学、北京市、100191、中国
抽象的な積層構造は複合材料において最も一般的に用いられる構成の一つであるが、層間特性の弱さから、層間剥離が主な破壊モードとなる。工学実務において一般的に用いられる多層積層板の層状化と膨張挙動に関する研究は、常に研究者にとってホットなテーマとなっている。本稿では、重慶大学と北京航空航天大学の疲労破壊実験室における炭素繊維強化複合材料の層間剥離に関する研究成果を、実験研究と数値シミュレーションの二つの側面から紹介する。最後に、この分野の発展方向を展望する。
キーワード:炭素繊維強化複合材、積層板、層間剥離、疲労層別化
導入
複合材料は、高い比強度、高い比剛性などの優れた特性を有し、航空宇宙、エネルギー技術、民間輸送、建設分野で広く利用されています。複合材料の加工および使用過程において、繊維とマトリックスは荷重下で様々な程度の損傷を受けます。複合積層板の一般的な破損モードには、層間損傷と層内損傷があります。厚さ方向の補強が不足しているため、積層板の横方向の機械的特性は劣っており、外部衝撃荷重下では層間剥離損傷が発生する可能性が高くなります。層状損傷の発生と拡大は、構造剛性と強度の低下につながり、壊滅的な事故を引き起こすこともあります。[1-3]そのため、複合材料の構造設計や強度解析において、剥離の問題はますます重要になってきており、複合材料の層状膨張挙動を研究する必要がある。[4].
積層板の層状膨張挙動に関する研究
1. 実験研究
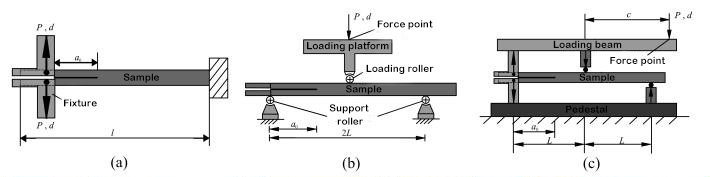
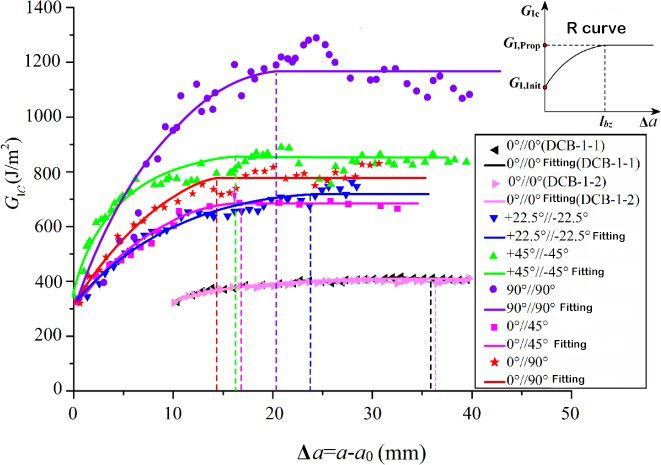
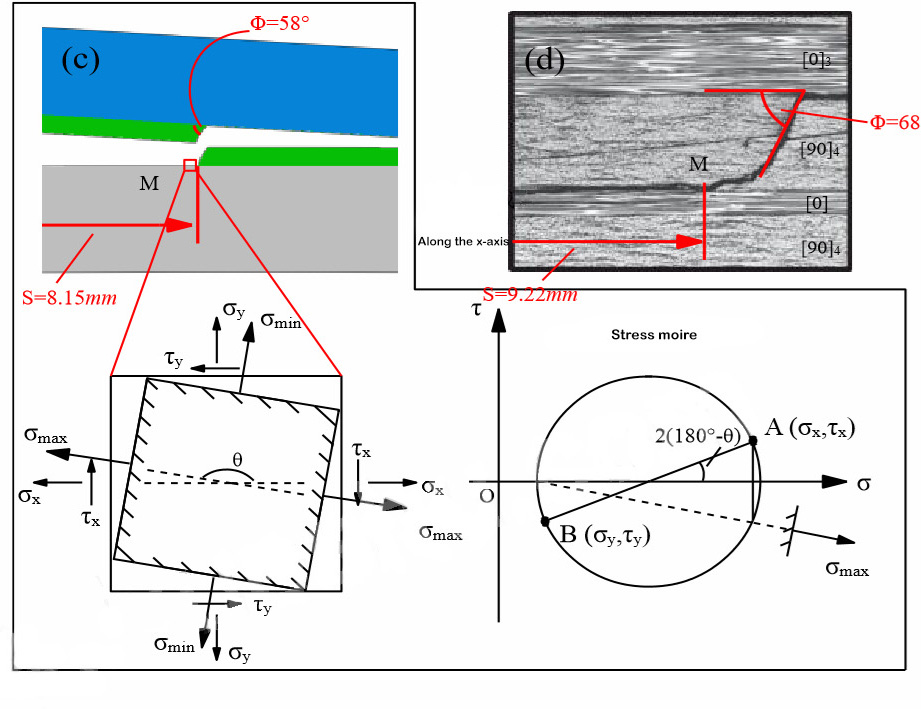
層間破壊靭性は、複合層間の機械的性質の特性パラメータです。タイプI、タイプII、およびI / IIハイブリッド一方向積層板の層間破壊靭性を測定するための対応する試験規格が確立されています。対応する試験装置を図1に示します。ただし、実際のエンジニアリング構造では、複合材料の多方向積層板がよく使用されます。そのため、多方向積層板の層化と膨張挙動に関する実験的研究は、より重要な理論的意義とエンジニアリング価値を持っています。多層積層板の層の開始と膨張は、任意の層角度の界面間で発生し、層状の膨張挙動は一方向積層板とは大きく異なり、膨張メカニズムはより複雑です。研究者による多方向積層板の実験研究は比較的少なく、層間破壊靭性の測定はまだ国際標準を確立していません。研究チームは、T700およびT800炭素繊維を用いて、界面積層角度の異なる様々な複合積層板を設計し、界面積層角度と繊維架橋が静的および疲労剥離挙動に及ぼす影響を研究した。その結果、層後縁によって形成される繊維架橋が層間破壊靭性に大きな影響を与えることが判明した。層状化が進むにつれて、層間破壊靭性は低い初期値から徐々に増加し、層状化が一定の長さに達すると安定値、すなわちR抵抗曲線現象に達する。層間層の初期破壊靭性は、樹脂の破壊靭性とほぼ等しく、これはマトリックス自体の破壊靭性に依存する。[5, 6]しかしながら、異なる界面における層間破壊靭性伸長値は大きく異なり、界面層角度に顕著な依存性が示されています。この依存性について、Zhaoらは、界面層角度が層間破壊靭性伸長に与える影響について検討しました。[5]層状抵抗源の物理的メカニズムに基づいて、層間破壊靭性安定値は2つの部分で構成され、1つは無関係な層界面の破壊仕事であり、もう1つは層内損傷と繊維の橋渡しによる破壊仕事であると考えられます。層状前面の応力前面場の有限要素解析を通じて、破壊仕事の2番目の部分は層間剥離前面損傷領域の深さに依存し(図3に示すように)、損傷領域の深さは界面の積層角度に比例することがわかりました。界面層角度の正弦関数で表されるI型破壊靭性安定値の理論モデルを提示します。
Gongら[7]異なる混合比におけるI/IIハイブリッド層状化試験を実施し、積層板におけるI/IIハイブリッド層状化も顕著なR抵抗曲線特性を示すことを明らかにした。異なる試験片間の破壊靭性を解析した結果、試験片の層間破壊靭性の初期値および安定値は、混合比の増加に伴い顕著に増加することが判明した。さらに、異なる混合比における層間層の初期および安定破壊靭性は、BK基準で記述できる。
疲労層別化の観点からは、試験中に顕著な繊維架橋も観察された。試験データの解析により、複合材料の疲労剥離拡大は「抵抗曲線」の影響を受けており、従来の疲労層別化拡大速度モデルと閾値はもはや適用できないことが判明した。張氏と彭氏は理論解析に基づき、[4,8,9]複合材料の疲労はく離拡大に必要なエネルギーを表すために、疲労はく離拡大抵抗を導入し、さらに正規化ひずみエネルギーを提案した。解放率は、疲労層状拡大速度モデルと制御パラメータの閾値である。このモデルと正規化閾値パラメータの適用性は実験によって検証されている。さらに、Zhaoらは、疲労はく離拡大抵抗を導入し、さらに正規化ひずみエネルギーを提案した。[3]繊維架橋、応力比、および荷重混合比が疲労成層化および膨張挙動に及ぼす影響を総合的に考慮し、応力比の影響を考慮した正規化疲労成層膨張速度モデルを構築した。このモデルの精度は、応力比および混合比の異なる疲労成層化試験によって検証された。正規化疲労成層膨張速度モデルにおける疲労成層膨張抵抗という物理量については、Gongらが報告している。[1]実験を通して限られた離散データ点しか得られないという計算方法の弱点を克服し、エネルギーの観点から疲労を解明する。層状伸張抵抗を計算するための解析モデルを構築する。このモデルは、疲労の層状化と伸張抵抗の定量的な評価を可能にし、提案された正規化疲労層状伸張速度モデルの適用に対する理論的裏付けを提供する。
図2 層間破壊靭性R抵抗曲線[5]
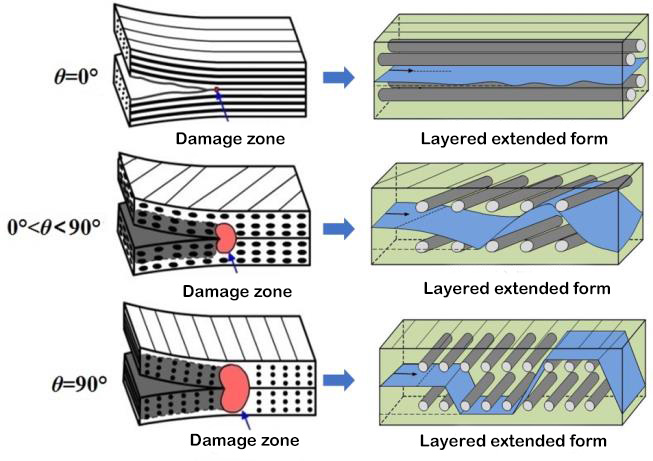
図3 層状の前縁損傷領域と層状の拡張形態[5]
2. 数値シミュレーション研究
層状膨張の数値シミュレーションは、複合構造設計分野における重要な研究内容である。複合材一方向積層板の層間剥離破壊を予測する場合、既存の層状膨張基準では、通常、層間破壊靭性定数を基本性能パラメータとして用いる。[10]き裂先端のエネルギー解放率と層間破壊靭性を比較することにより、層状構造が拡大しているかどうかを判断します。多方向積層板の破壊メカニズムは複雑です。[11,12]顕著なR抵抗曲線を特徴とする[5,13]既存の層状膨張基準ではこの特徴が考慮されておらず、繊維含有架橋多方向積層板の層間剥離挙動のシミュレーションには適用されない。Gong et al.[10、13]既存の層状膨張基準を改良し、R抵抗曲線を基準に導入することを提案し、これに基づいて、繊維架橋の影響を考慮した層状膨張基準を確立した。双線形構成結合力単位の定義と使用パラメータは、初期界面剛性、界面強度、粘性係数、および結合力領域内の最小要素数など、数値的手法によって体系的に研究された。対応する結合力単位パラメータモデルが確立された。最後に、改良された層状膨張基準と結合力単位パラメータモデルの有効性と適用性は、静的成層試験によって検証された。しかし、改良された基準は、位置依存性のため1次元の層状シミュレーションにのみ使用でき、2次元または3次元の階層的拡張には使用できない。この問題を解決するために、著者はさらに、繊維架橋を考慮した新しい3線形結合力構成を提案した。[14]構成関係は、微視的な視点から層状膨張の複雑な過程に適合し、パラメータが単純で物理的意味が明確であるという利点がある。
さらに、多方向積層板の層化プロセスでよく見られる層状移動現象を正確にシミュレートするために、[11,12]、Zhao et al.[11,12]拡張有限要素法に基づく亀裂経路誘導モデルを提案し、特殊設計をシミュレートしました。複合材成層試験における階層的移行。同時に、90°/90°層状界面に沿ったジグザグ層状膨張挙動を予測する層状膨張モデルを提案し、90°/90°界面の層状膨張挙動を高精度にシミュレートしました。
結論
本論文では、本研究グループの複合積層板はく離分野における研究成果に焦点を当てています。実験面では、主に界面レイアップ角度と繊維架橋が静的および疲労はく離膨張挙動に及ぼす影響について検討しています。多数の実験研究を通じて、複合材料の多方向積層板の破壊メカニズムは複雑であることがわかりました。繊維架橋は多方向積層板の一般的な強靭化メカニズムであり、層間破壊靭性のR抵抗曲線の主な原因です。現在、II層化におけるR抵抗曲線の研究は比較的不足しており、さらなる研究が必要です。破壊メカニズムから出発して、さまざまな影響因子を含む疲労層化モデルを提案し、これが疲労層化研究の方向性を示しています。数値シミュレーションの面では、研究グループは、繊維架橋が層状膨張挙動に及ぼす影響を考慮するために、改良された階層的膨張基準と凝集構成モデルを提案しました。さらに、拡張有限要素を用いることで、階層的移動現象をより適切にシミュレートできます。この手法は、微細なセル分割を必要としないため、メッシュの再分割に伴う問題を解消できます。任意形状の成層化をシミュレートする上で独自の利点があり、今後、この手法の工学応用研究をさらに進める必要があります。[16].
参考文献
[1] Y Gong、L Zhao、J Zhang、N Hu. エネルギーの観点から複合積層板の疲労はく離抵抗を決定するための新しいモデル. Compos Sci Technol 2018; 167: 489-96.
[2] L Zhao、Y Wang、J Zhang、Y Gong、N Hu、N Li. モードI荷重下における積層複合材料のジグザグ剥離の成長をシミュレーションするためのXFEMベースモデル. Compos Struct 2017; 160: 1155-62.
[3] L Zhao, Y Gong, J Zhang, Y Wang, Z Lu, L Peng, N Hu. CFRP多方向積層板における疲労はく離成長挙動の新しい解釈. Compos Sci Technol 2016; 133: 79-88.
[4] L Peng、J Zhang、L Zhao、R Bao、H Yang、B Fei。疲労荷重下における多方向複合積層板のモードIはく離の進行。J Compos Mater 2011; 45: 1077-90。
[5] L Zhao, Y Wang, J Zhang, Y Gong, Z Lu, N Hu, J Xu. モードI荷重下における多方向CFRP積層板のプラトー破壊靭性の界面依存モデル.複合材料パートB:エンジニアリング2017; 131: 196-208.
[6] L Zhao, Y Gong, J Zhang, Y Chen, B Fei. 結合要素を用いたモードIおよび混合モードI/II荷重下における多方向積層板のはく離進展シミュレーション. Compos Struct 2014; 116: 509-22.
[7] Y Gong、B Zhang、L Zhao、J Zhang、N Hu、C Zhang。一方向および多方向界面を持つカーボン/エポキシ積層板の混合モードI/II剥離のR曲線挙動。Compos Struct 2019。(審査中)。
[8] L Peng、J Xu、J Zhang、L Zhao。疲労荷重下における多方向複合積層板の混合モードはく離成長。Eng Fract Mech 2012; 96: 676-86。
[9] J Zhang, L Peng, L Zhao, B Fei. 混合モード荷重下における複合材料積層板の疲労はく離成長速度と閾値. Int J Fatigue 2012; 40: 7-15.
[10] Y Gong、L Zhao、J Zhang、Y Wang、N Hu. CFRP多方向積層板の混合モードI/II層間剥離に対する繊維ブリッジングの影響を考慮した層間剥離伝播基準. Compos Sci Technol 2017; 151: 302-9.
[11] Y Gong、B Zhang、SR Hallett. モードI準静的および疲労荷重下における多方向複合積層板の層間剥離の移動. Compos Struct 2018; 189: 160-76.
[12] Y Gong、B Zhang、S Mukhopadhyay、SR Hallett。モードII静的および疲労荷重下における多方向積層板の層間剥離移動に関する実験的研究、モードIとの比較。Compos Struct 2018; 201: 683-98。
[13] Y Gong、L Zhao、J Zhang、N Hu. 複合材料多方向積層板における大規模繊維橋渡しを考慮した層間剥離伝播の改良べき乗則基準. Compos Struct 2018; 184: 961-8.
[14] Y Gong、Y Hou、L Zhao、W Li、G Yang、J Zhang、N Hu. 繊維架橋を考慮したDCB積層板の剥離進展に関する新しい3線形接着領域モデル. Compos Struct 2019. (投稿予定)
[15] L Zhao、J Zhi、J Zhang、Z Liu、N Hu. 複合材料積層板の層間剥離のXFEMシミュレーション. 複合材料パートA:応用科学と製造 2016; 80: 61-71.
[16] 趙立斌、龔宇、張建宇. 繊維強化複合材料積層板の層状膨張挙動に関する研究の進展. 航空科学ジャーナル 2019: 1-28.
ソース:Gong Yu、Wang Yana、Peng Lei、Zhao Libin、Zhang Jianyu. 先進炭素繊維強化複合材料積層板の層状膨張挙動に関する研究[C]. 力学と工学 - 数値計算とデータ分析 2019 学術会議. 中国機械学会、北京機械学会、2019年. 経由 学書
投稿日時: 2019年11月15日