מכניקה והנדסה - חישוב מספרי וניתוח נתונים
כנס אקדמי למכניקה והנדסה - חישובים מספריים וניתוח נתונים 2019, 19-21 באפריל, 2019, בייג'ינג
19-21 באפריל, 2019, בייג'ינג, סין
מחקר על התנהגות התפשטות שכבתית של יריעת למינציה מרוכבת מחוזקת בסיבי פחמן מתקדמת
גונג יו1*וואנג יאנה2, פנג ליי3, ז'או ליבין4, ג'אנג ג'יאניו1
1אוניברסיטת צ'ונגצ'ינג, צ'ונגצ'ינג, 400044, סין
2מכון המחקר לתעופה של סין, מכון המחקר לחומרי אווירונאוטיקה של בייג'ינג, בייג'ינג, 100095, סין
3מרכז המחקר לטכנולוגיית מטוסים אזרחיים של בייג'ינג, בייג'ינג, 102211, סין
4אוניברסיטת בייג'ינג לאווירונאוטיקה ואסטרונאוטיקה, בייג'ינג, 100191, סין
תַקצִירמבנה הלמינציה הוא אחת מתצורות הקומפוזיט הנפוצות ביותר עבור חומרים מרוכבים, אך דה-למינציה הופכת למצב הכשל העיקרי שלה עקב תכונות חלשות של השכבות הבין-למינריות. מחקר על ריבוד והתנהגות התפשטות של למינציה רב-שכבתית הנפוצות בפרקטיקה ההנדסית תמיד היה נושא חם עבור חוקרים. במאמר זה, מוצגות תוצאות המחקר של דה-למינציה של קומפוזיט מחוזק בסיבי פחמן באוניברסיטת צ'ונגצ'ינג ובמעבדה לשברי עייפות של אוניברסיטת בייג'ינג לאווירונאוטיקה ואסטרונאוטיקה משני היבטים של מחקר ניסיוני וסימולציה נומרית. לבסוף, נבחן כיוון הפיתוח של התחום.
מילות מפתח:מרוכב מחוזק בסיבי פחמן, למינציה, דה-למינציה, ריבוד עייפות
מָבוֹא
לחומרים מרוכבים תכונות מצוינות כגון חוזק סגולי גבוה וקשיחות סגולית גבוהה, והם נמצאים בשימוש נרחב בתעשיית התעופה והחלל, טכנולוגיית האנרגיה, התחבורה האזרחית והבנייה. במהלך עיבוד ושימוש בחומרים מרוכבים, הסיבים והמטריצה יעברו דרגות שונות של נזק תחת עומס. מצבי כשל נפוצים עבור למינציות מרוכבות כוללים נזק בין שכבות ונזק בתוך שכבות. עקב היעדר חיזוק בכיוון העובי, התכונות המכניות הצידיות של הלמינציה גרועות, וסביר מאוד שיתרחש נזק מהתפרקות תחת עומסי פגיעה חיצוניים. התרחשות והתפשטות של נזק מרובד יובילו לירידה בקשיחות ובחוזק המבני, ואף יגרמו לתאונות קטסטרופליות.[1-3]לכן, בעיית הפירוק מודאגת יותר ויותר על ידי תכנון מבני וניתוח חוזק של חומרים מרוכבים, ויש צורך ללמוד את התנהגות ההתפשטות השכבתית של חומרים מרוכבים.[4].
מחקר על התנהגות התפשטות שכבתית של למינציה
1. מחקר ניסיוני
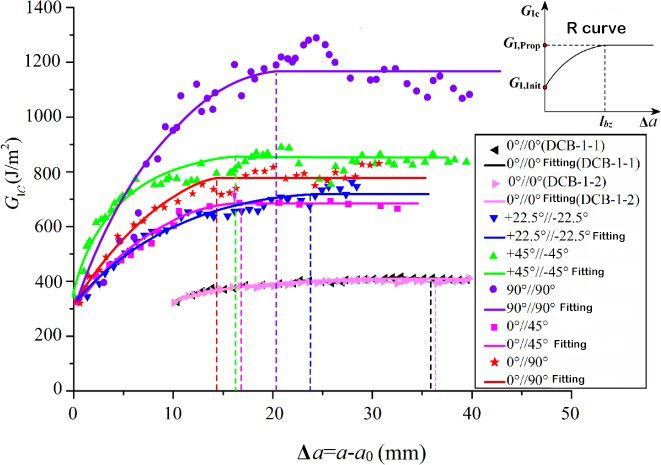
קשיחות שבר בין-שכבתי היא פרמטר אופייני לתכונות המכניות בין שכבות מרוכבות. סטנדרטים מתאימים לבדיקה נקבעו לקביעת קשיחות שבר בין-שכבתי של למינטים חד-כיווניים היברידיים מסוג I, סוג II ו-I/II. מנגנון הבדיקה המתאים מוצג באיור 1. עם זאת, למינטים רב-כיווניים של חומרים מרוכבים משמשים לעתים קרובות במבנה ההנדסי בפועל. לכן, למחקר הניסויי על התנהגות הריבוד וההתפשטות של למינטים רב-כיווניים יש משמעות תיאורטית וערך הנדסי חשובים יותר. התחלה והתפשטות של שכבות למינט רב-שכבתיות מתרחשות בין ממשקים עם זוויות שכבה שרירותיות, והתנהגות ההתפשטות השכבתית שונה משמעותית מזו של למינטים חד-כיווניים, ומנגנון ההתפשטות מסובך יותר. לחוקרים יש מעט יחסית מחקרים ניסויים על למינטים רב-כיווניים, וקביעת קשיחות שבר בין-שכבתי טרם קבעה תקן בינלאומי. צוות המחקר השתמש בסיבי פחמן T700 ו-T800 כדי לתכנן מגוון למינטים מרוכבים עם זוויות פריסת ממשק שונות, וחקר את השפעת זווית פריסת הממשק וגישור הסיבים על התנהגות פירוק סטטי ועייפות. נמצא כי גישור סיבים הנוצר על ידי הקצה האחורי של השכבה משפיע רבות על קשיחות השבר הבין-שכבתית. ככל שהריבוד מתרחב, קשיחות השבר הבין-שכבתית תגדל בהדרגה מערך התחלתי נמוך יותר, וכאשר הריבוד מגיע לאורך מסוים, הוא מגיע לערך יציב, כלומר, תופעת עקומת ההתנגדות R. קשיחות השבר ההתחלתית של השכבה הבין-שכבתית כמעט שווה ובקירוב לקשיחות השבר של השרף, התלויה בקשיחות השבר של המטריצה עצמה.[5, 6]עם זאת, ערכי ההתארכות של קשיחות השבר הבין-שכבתית של ממשקים שונים משתנים מאוד. מוצגת תלות משמעותית בזווית שכבת הממשק. בתגובה לתלות זו, ז'או ואח'.[5]בהתבסס על המנגנון הפיזי של מקור ההתנגדות המרובד, נלקח בחשבון שערך יציבות קשיחות השבר הבין-שכבתי מורכב משני חלקים, חלק אחד הוא עבודת השבר של ממשק השכבה הלא קשור, והחלק השני הוא הנזק התוך-שכבתי והסיב. עבודת השבר הנגרמת על ידי גישור. באמצעות ניתוח אלמנטים סופיים של שדה חזית המאמץ של החזית השכבתית, נמצא שהחלק השני של עבודת השבר תלוי בעומק אזור הנזק של חזית הדה-למינציה (כפי שמוצג באיור 3), ועומק אזור הנזק פרופורציונלי לזווית פריסת הממשק. מוצג מודל תיאורטי של ערך יציבות קשיחות השבר מסוג I המתבטא בפונקציה הסינוסואידלית של זווית שכבת הממשק.
גונג ואחרים.[7]ביצענו את מבחן הריבוד ההיברידי I/II תחת יחסי ערבוב שונים, ומצאו כי לריבוד ההיברידי I/II בלמינציה יש גם מאפייני עקומת התנגדות R משמעותיים. באמצעות ניתוח קשיחות השבר בין חלקי בדיקה שונים, נמצא כי הערך ההתחלתי והערך היציב של קשיחות השבר הבין-שכבתית של חלקי הבדיקה עולים משמעותית עם עליית יחס הערבוב. בנוסף, ניתן לתאר את קשיחות השבר ההתחלתית והיציבה של השכבה הבין-שכבתית תחת יחסי ערבוב שונים באמצעות קריטריון BK.
מבחינת ריבוד עייפות, נצפתה גם גישור משמעותי של סיבים במהלך הבדיקה. באמצעות ניתוח נתוני הבדיקה, נמצא כי התפשטות הפירוק עקב עייפות של החומר המרוכב מושפעת מ"עקומת ההתנגדות", כך שמודל קצב התפשטות ריבוד העייפות המסורתי וערך הסף אינם ישימים עוד. על סמך ניתוח תיאורטי, ג'אנג ופנג[4,8,9]הציגו את התנגדות ההתפשטות עקב דה-למינציה עייפות כדי לבטא את האנרגיה הנדרשת להתפשטות עקב דה-למינציה עייפות של חומרים מרוכבים, והציעו בנוסף את אנרגיית המאמץ המנורמלת. קצב השחרור הוא מודל קצב ההתפשטות המרובד עקב עייפות וערך הסף של פרמטרי הבקרה. תחולת המודל ופרמטר הסף המנורמל אומתה על ידי ניסויים. יתר על כן, ז'או ואח'.[3]בחנו באופן מקיף את השפעות גישור הסיבים, יחס המאמץ ויחס ערבוב העומס על התנהגות ריבוד והתפשטות עייפות, ויצרו מודל קצב התפשטות מרובד עייפות מנורמל תוך התחשבות בהשפעת יחס המאמץ. דיוק המודל אומת על ידי מבחני ריבוד עייפות עם יחסי מאמץ ויחסי ערבוב שונים. עבור הכמות הפיזיקלית של התנגדות התפשטות מרובדת עייפות במודל קצב התפשטות מרובד עייפות מנורמל, Gong et al.[1]להתגבר על חולשת שיטת החישוב שיכולה להשיג רק נקודות נתונים דיסקרטיות מוגבלות באמצעות ניסויים, ולקבוע עייפות מנקודת מבט אנרגטית. מודל אנליטי לחישוב התנגדות מורחבת מרובדת. המודל יכול לממש את הקביעה הכמותית של ריבוד עייפות ועמידות התפשטות, ולספק תמיכה תיאורטית ליישום מודל קצב ההתפשטות המרובדת המנורמל של עייפות.
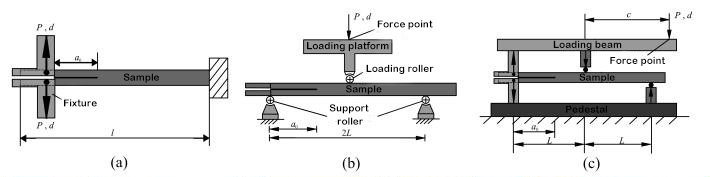 איור 1 דיאגרמת מכשיר בדיקה מרובד
איור 1 דיאגרמת מכשיר בדיקה מרובד
איור 2 עקומת התנגדות R לקשיחות שבר בין שכבות[5]
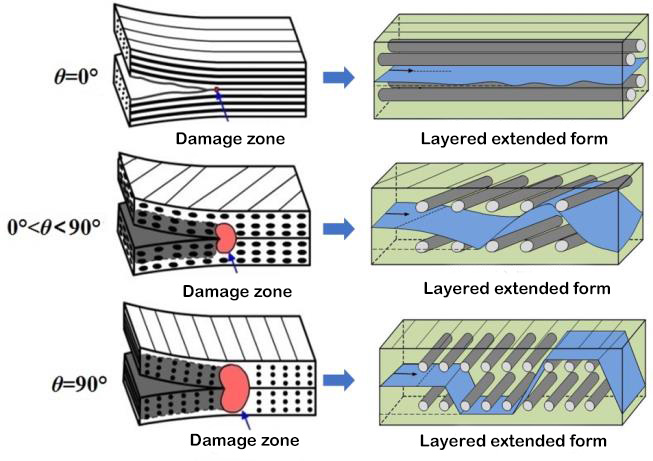
איור 3 אזור נזק שכבתי בקצה הקדמי ומורפולוגיה מורחבת מרובדת[5]
2. מחקר סימולציה נומרית
סימולציה נומרית של התפשטות שכבתית היא תוכן מחקר חשוב בתחום תכנון מבנים מרוכבים. כאשר ניבוי כשל דה-למינציה של למינטים חד-כיווניים מרוכבים, קריטריוני התפשטות הריבוד הקיימים משתמשים בדרך כלל בקשיחות שבר בין-שכבתית קבועה כפרמטר הביצועים הבסיסי.[10], על ידי השוואת קצב שחרור האנרגיה של קצה הסדק וקשיחות השבר הבין-שכבתי. גודל כדי לקבוע אם השכבות מתרחבות. מנגנון הכשל של למינציות רב-כיווניות הוא מורכב.[11,12], המאופיין בעקומות התנגדות R משמעותיות[5,13]קריטריוני ההתפשטות השכבתית הקיימים אינם מתחשבים במאפיין זה ואינם חלים על סימולציית התנהגות הדה-למינציה של למינטים רב-כיווניים מגושרים המכילים סיבים. גונג ואחרים.[10, 13]שיפרו את קריטריוני ההתפשטות המרובדים הקיימים והציעו להכניס את עקומת ההתנגדות R לקריטריונים, ועל סמך זה, קבעו קריטריון התפשטות מרובד תוך התחשבות בהשפעות גישור הסיבים. פרמטרי ההגדרה והשימוש של היחידה הקוהזיבית הקונסטיטוטיבית הדו-לינארית נחקרו באופן שיטתי באמצעות שיטות נומריות, כולל קשיחות הממשק ההתחלתית, חוזק הממשק, מקדם הצמיגות ומספר האלמנטים המינימלי באזור הכוח הקוהזיבי. נקבע מודל פרמטר היחידה הקוהזיבית המתאים. לבסוף, האפקטיביות והישימות של קריטריון ההתפשטות השכבתית המשופר ומודל פרמטר היחידה הקוהזיבית אומתו על ידי מבחן ריבוד סטטי. עם זאת, ניתן להשתמש בקריטריונים המשופרים רק עבור סימולציות שכבות חד-ממדיות עקב תלות מיקום ולא עבור הרחבות היררכיות דו-ממדיות או תלת-ממדיות. על מנת לפתור בעיה זו, המחבר הציע עוד כוח קוהזיבי תלת-לינארי חדש תוך התחשבות בגישור סיבים.[14]הקשר המכון מתאים לתהליך המורכב של התפשטות שכבתית מנקודת מבט מיקרוסקופית, ויש לו יתרונות של פרמטרים פשוטים ומשמעות פיזיקלית ברורה.
בנוסף, על מנת לדמות במדויק את תופעת הנדידה המרובדת הנפוצה בתהליך הריבוד של למינציות רב-כיווניות[11,12], ז'או ואחרים.[11,12]הציע מודל הנחיית מסלול סדק המבוסס על אלמנטים סופיים מורחבים, המדמה תכנון מיוחד. נדידה היררכית במבחן ריבוד מורכב. במקביל, מוצע מודל התפשטות שכבתי עבור התנהגות ההתפשטות השכבתית בזיגזג לאורך הממשק השכבתי 90°/90°, אשר מדמה במדויק את התנהגות ההתפשטות השכבתית של הממשק 90°/90°.
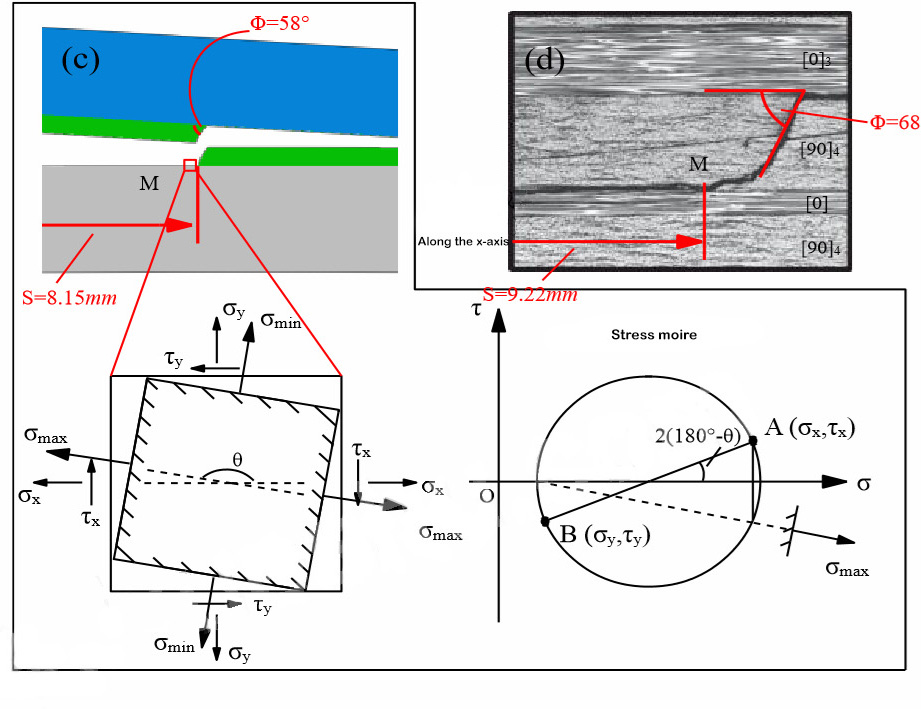 איור 4 סימולציה נומרית של נדידת שכבות ותוצאות ניסוייות[15]
איור 4 סימולציה נומרית של נדידת שכבות ותוצאות ניסוייות[15]
מַסְקָנָה
מאמר זה מתמקד בתוצאות המחקר של קבוצה זו בתחום פירוק הלמינציה המרוכבת. ההיבטים הניסויים כוללים בעיקר את השפעת זווית השכבה של הממשק וגישור הסיבים על התנהגות ההתפשטות הסטטית והעייפות. באמצעות מספר רב של מחקרים ניסויים, נמצא כי מנגנון הכשל הרב-כיווני של הלמינציה של חומרים מרוכבים הוא מסובך. גישור סיבים הוא מנגנון הקשחה נפוץ של למינציות רב-כיווניות, שהוא הסיבה העיקרית לעקומת ההתנגדות R של קשיחות שבר בין-שכבתי. נכון לעכשיו, מחקר עקומת ההתנגדות R תחת ריבוד II חסר יחסית וזקוק למחקר נוסף. החל ממנגנון הכשל, מוצע מודל ריבוד עייפות הכולל גורמי השפעה שונים, שהוא כיוון למחקר ריבוד עייפות. מבחינת סימולציה נומרית, קבוצת המחקר הציעה קריטריון התפשטות היררכי משופר ומודל מכונן קוהרנטי כדי לבחון את השפעת גישור הסיבים על התנהגות ההתפשטות המרובדת. בנוסף, האלמנט הסופי המורחב משמש לסימולציה טובה יותר של תופעת הנדידה ההיררכית. שיטה זו מבטלת את הצורך בחלוקת תאים עדינה, ובכך מבטלת את הבעיות הקשורות לחלוקה מחדש של הרשת. יש לה יתרונות ייחודיים בסימולציה של ריבוד של צורות שרירותיות, ונדרש מחקר יישומי הנדסי נוסף של שיטה זו בעתיד.[16].
הפניות
[1] Y Gong, L Zhao, J Zhang, N Hu. מודל חדש לקביעת עמידות לדה-למינציה עקב עייפות בלמינציות מרוכבות מנקודת מבט של אנרגיה. Compos Sci Technol 2018; 167: 489-96.
[2] L Zhao, Y Wang, J Zhang, Y Gong, N Hu, N Li. מודל מבוסס XFEM לסימולציה של צמיחת דה-למינציה זיגזג בחומרים מרוכבים למינציה תחת טעינה במצב I. Compos Struct 2017; 160: 1155-62.
[3] ל. ז'או, י. גונג, ג'. ז'אנג, י. וואנג, ז. לו, ל. פנג, נ. הו. פרשנות חדשנית של התנהגות גדילה עקב עייפות בלמינציות רב-כיווניות של CFRP. Compos Sci Technol 2016; 133: 79-88.
[4] L Peng, J Zhang, L Zhao, R Bao, H Yang, B Fei. גידול דה-למינציה במצב I של למינציות מרוכבות רב-כיווניות תחת עומס עייפות. J Compos Mater 2011; 45: 1077-90.
[5] L Zhao, Y Wang, J Zhang, Y Gong, Z Lu, N Hu, J Xu. מודל תלוי-ממשק של קשיחות שבר מפלטו בלמינציות CFRP רב-כיווניות תחת עומס במצב I. חומרים מרוכבים חלק ב': הנדסה 2017; 131: 196-208.
[6] L Zhao, Y Gong, J Zhang, Y Chen, B Fei. סימולציה של צמיחת דה-למינציה בלמינציות רב-כיווניות תחת עומסים במצב I ובמצב מעורב I/II באמצעות אלמנטים קוהזיביים. Compos Struct 2014; 116: 509-22.
[7] Y Gong, B Zhang, L Zhao, J Zhang, N Hu, C Zhang. התנהגות עקומת R של דה-למינציה I/II במצב מעורב בלמינציות פחמן/אפוקסי עם ממשקים חד-כיווניים ורב-כיווניים. Compos Struct 2019. (בסקירה).
[8] L Peng, J Xu, J Zhang, L Zhao. גידול דה-למינציה במצב מעורב של למינציות מרוכבות רב-כיווניות תחת עומס עייפות. Eng Fract Mech 2012; 96: 676-86.
[9] J Zhang, L Peng, L Zhao, B Fei. קצבי גדילה וספי גדילה עקב עייפות של למינציות מרוכבות תחת עומס מעורב. Int J Fatigue 2012; 40: 7-15.
[10] Y Gong, L Zhao, J Zhang, Y Wang, N Hu. קריטריון התפשטות דה-למינציה כולל השפעת גישור סיבים עבור דה-למינציה במצב מעורב I/II בלמינציות רב-כיווניות CFRP. Compos Sci Technol 2017; 151: 302-9.
[11] Y Gong, B Zhang, SR Hallett. נדידת דה-למינציה בלמינציות מרוכבות רב-כיווניות תחת עומס קוואזי-סטטי ועייפות במצב I. Compos Struct 2018; 189: 160-76.
[12] Y Gong, B Zhang, S Mukhopadhyay, SR Hallett. מחקר ניסיוני על נדידת דה-למינציה בלמינציות רב-כיווניות תחת עומס סטטי ועייפות במצב II, עם השוואה למצב I. Compos Struct 2018; 201: 683-98.
[13] Y Gong, L Zhao, J Zhang, N Hu. קריטריון משופר של חוק החזקה להתפשטות דה-למינציה עם השפעת גישור סיבים בקנה מידה גדול בלמינציות מרוכבות רב-כיווניות. Compos Struct 2018; 184: 961-8.
[14] Y Gong, Y Hou, L Zhao, W Li, G Yang, J Zhang, N Hu. מודל חדשני של אזורים קוהזיביים תלת-לינאריים לצמיחת דה-למינציה בלמינציות DCB עם השפעת גישור סיבים. Compos Struct 2019. (יש להגיש)
[15] L Zhao, J Zhi, J Zhang, Z Liu, N Hu. סימולציית XFEM של דה-למינציה בלמינציות מרוכבות. חומרים מרוכבים חלק א': מדע יישומי וייצור 2016; 80: 61-71.
[16] ז'או ליבין, גונג יו, ג'אנג ג'יאניו. התקדמות המחקר על התנהגות התפשטות מרובדת של למינציות מרוכבות מחוזקות בסיבים. כתב העת למדעי האווירונאוטיקה 2019: 1-28.
מָקוֹר:גונג יו, וואנג יאנה, פנג ליי, ז'או ליבין, ג'אנג ג'יאניו. מחקר על התנהגות התפשטות מרובדת של למינציות מרוכבות מחוזקות בסיבי פחמן מתקדמות [C]. מכניקה והנדסה - כנס אקדמי חישוב נומרי וניתוח נתונים 2019. החברה הסינית למכניקה, החברה המכנית של בייג'ינג, 2019. בְּאֶמצָעוּת איקסושו
זמן פרסום: 15 בנובמבר 2019