Estudio sobre el comportamiento de expansión en capas de láminas compuestas reforzadas con fibra de carbono avanzada

MECÁNICA E INGENIERÍA - Cálculo numérico y análisis de datos
Conferencia Académica de Mecánica e Ingeniería: Cálculos Numéricos y Análisis de Datos 2019, del 19 al 21 de abril de 2019, Pekín
19-21 de abril de 2019, Pekín, China

Estudio sobre el comportamiento de expansión en capas de láminas compuestas reforzadas con fibra de carbono avanzada

Gong Yu^1*, Wang Yana², Peng Lei³, Zhao Libin⁴, Zhang Jianyu¹

¹Universidad de Chongqing, Chongqing, 400044, China
²Instituto de Investigación de Aviación de China, Instituto de Investigación de Materiales Aeronáuticos de Beijing, Beijing, 100095, China
³Centro de Investigación de Tecnología de Aeronaves Civiles de Beijing, Beijing, 102211, China
⁴Universidad de Aeronáutica y Astronáutica de Beijing, Beijing, 100191, China

AbstractoLa estructura laminada es una de las configuraciones de compuestos más utilizadas, pero la delaminación se convierte en su principal modo de fallo debido a las débiles propiedades interlaminares. La investigación sobre el comportamiento de estratificación y expansión de laminados multicapa, comúnmente utilizado en la práctica de la ingeniería, siempre ha sido un tema de gran interés para los académicos. En este artículo, se presentan los resultados de la investigación sobre la delaminación de compuestos reforzados con fibra de carbono en la Universidad de Chongqing y el Laboratorio de Fractura por Fatiga de la Universidad de Aeronáutica y Astronáutica de Pekín, desde dos perspectivas: la investigación experimental y la simulación numérica. Finalmente, se prospecta la dirección de desarrollo de este campo.

Palabras clave:Compuesto reforzado con fibra de carbono, laminado, delaminación, estratificación por fatiga

introducción

Los materiales compuestos poseen excelentes propiedades, como alta resistencia y rigidez específicas, y se han utilizado ampliamente en la industria aeroespacial, la tecnología energética, el transporte civil y la construcción. Durante el procesamiento y uso de materiales compuestos, las fibras y la matriz sufren diferentes grados de daño bajo carga. Los modos de fallo comunes de los laminados compuestos incluyen daños entre capas y daños dentro de las capas. Debido a la falta de refuerzo en la dirección del espesor, las propiedades mecánicas laterales del laminado son deficientes, y es muy probable que se produzcan daños por delaminación bajo cargas de impacto externas. La aparición y expansión de daños estratificados conlleva una disminución de la rigidez y resistencia estructural, e incluso puede causar accidentes catastróficos.^[1-3]Por lo tanto, el problema de la delaminación es cada vez más importante en el diseño estructural y el análisis de resistencia de los materiales compuestos, y es necesario estudiar su comportamiento de expansión estratificada.^[4].

Investigación sobre el comportamiento de expansión en capas del laminado
1. Estudio experimental

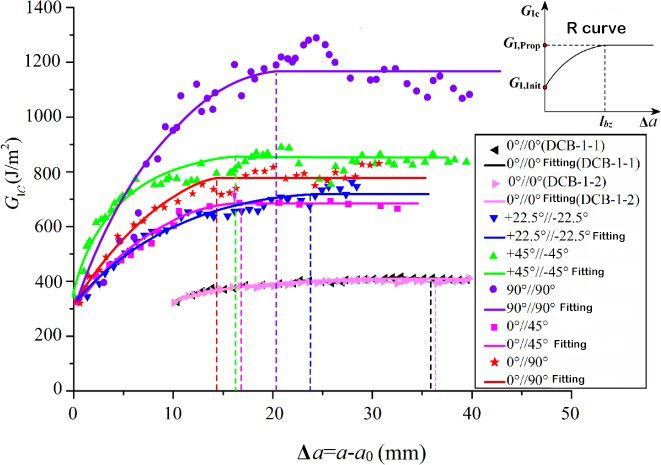
La tenacidad a la fractura interlaminar es un parámetro característico de las propiedades mecánicas entre capas compuestas. Se han establecido estándares de prueba correspondientes para la determinación de la tenacidad a la fractura interlaminar de laminados unidireccionales híbridos Tipo I, Tipo II y I/II. El aparato de prueba correspondiente se muestra en la Figura 1. Sin embargo, los laminados multidireccionales de materiales compuestos se utilizan a menudo en la estructura de ingeniería real. Por lo tanto, el estudio experimental sobre el comportamiento de estratificación y expansión de laminados multidireccionales tiene mayor importancia teórica y valor de ingeniería. La iniciación y expansión de la capa del laminado multicapa ocurren entre interfaces con ángulos de estratificación arbitrarios, y el comportamiento de expansión por capas es significativamente diferente al de los laminados unidireccionales, y el mecanismo de expansión es más complejo. Los investigadores tienen relativamente pocos estudios experimentales sobre laminados multidireccionales, y la determinación de la tenacidad a la fractura interlaminar aún no ha establecido un estándar internacional. El equipo de investigación utilizó fibra de carbono T700 y T800 para diseñar diversos laminados compuestos con diferentes ángulos de laminado de interfaz y estudió la influencia de estos y la formación de puentes de fibra en el comportamiento de delaminación estática y por fatiga. Se ha descubierto que los puentes de fibra formados por el borde de salida de la capa tienen una gran influencia en la tenacidad a la fractura interlaminar. A medida que la estratificación se expande, esta tenacidad aumenta gradualmente desde un valor inicial más bajo, y cuando la estratificación alcanza cierta longitud, alcanza un valor estable, es decir, el fenómeno de la curva de resistencia R. La tenacidad a la fractura inicial de la intercapa es casi igual y aproximadamente igual a la tenacidad a la fractura de la resina, que depende de la tenacidad a la fractura de la propia matriz.^{[5, 6]}Sin embargo, los valores de extensión de la tenacidad de fractura interlaminar de diferentes interfaces varían considerablemente. Se presenta una dependencia significativa del ángulo de la capa de interfaz. En respuesta a esta dependencia, Zhao et al.^[5]Con base en el mecanismo físico de la fuente de resistencia estratificada, se considera que el valor de estabilidad de la tenacidad a la fractura interlaminar consta de dos partes: una parte corresponde al trabajo de fractura de la interfaz de la capa no relacionada y la otra al daño intracapa y la fibra. El trabajo de fractura causado por el puenteo. Mediante el análisis de elementos finitos del campo del frente de tensión del frente estratificado, se observa que la segunda parte del trabajo de fractura depende de la profundidad de la zona de daño del frente de delaminación (como se muestra en la Figura 3), y la profundidad de la zona de daño es proporcional al ángulo de laminación de la interfaz. Se presenta un modelo teórico del valor de estabilidad de la tenacidad a la fractura de tipo I expresado por la función sinusoidal del ángulo de la capa de la interfaz.
Gong y otros.^[7]Se realizó la prueba de estratificación híbrida I/II con diferentes proporciones de mezcla y se observó que la estratificación híbrida I/II en el laminado también presenta características significativas de la curva de resistencia R. Mediante el análisis de la tenacidad a la fractura entre diferentes probetas, se observó que el valor inicial y el valor estable de la tenacidad a la fractura interlaminar de la probeta aumentan significativamente con el aumento de la proporción de mezcla. Además, la tenacidad a la fractura inicial y estable de la intercapa con diferentes proporciones de mezcla puede describirse mediante el criterio BK.
En cuanto a la estratificación por fatiga, también se observó una importante formación de puentes de fibras durante la prueba. El análisis de los datos de la prueba revela que la expansión por delaminación por fatiga del material compuesto se ve afectada por la "curva de resistencia", por lo que el modelo tradicional de tasa de expansión por estratificación por fatiga y el valor umbral ya no son aplicables. Con base en el análisis teórico, Zhang y Peng^[4,8,9]Introdujeron la resistencia a la expansión por delaminación por fatiga para expresar la energía requerida para la expansión por delaminación por fatiga de materiales compuestos, y propusieron además la energía de deformación normalizada. La tasa de liberación es el modelo de tasa de expansión estratificada por fatiga y el valor umbral de los parámetros de control. La aplicabilidad del modelo y del parámetro umbral normalizado se verifica mediante experimentos. Además, Zhao et al.^[3]Se analizaron exhaustivamente los efectos del puenteo de fibras, la relación de tensiones y la relación de mezcla de cargas en la estratificación por fatiga y el comportamiento de expansión, y se estableció un modelo normalizado de tasa de expansión estratificada por fatiga considerando la influencia de la relación de tensiones. La precisión del modelo se verificó mediante ensayos de estratificación por fatiga con diferentes relaciones de tensiones y relaciones de mezcla. Para la magnitud física de la resistencia a la expansión estratificada por fatiga en el modelo normalizado de tasa de expansión estratificada por fatiga, Gong et al.^[1]Superar la debilidad del método de cálculo, que solo permite obtener datos discretos limitados mediante experimentos, y determinar la fatiga desde el punto de vista energético. Se creó un modelo analítico para el cálculo de la resistencia extendida estratificada. Este modelo permite la determinación cuantitativa de la estratificación por fatiga y la resistencia a la expansión, y proporciona fundamento teórico para la aplicación del modelo de tasa de expansión estratificada por fatiga normalizada propuesto.

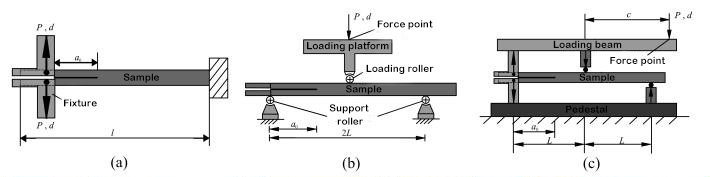Figura 1 Diagrama del dispositivo de prueba estratificado

Figura 2 Curva de resistencia a la tenacidad a la fractura entre capas R^[5]


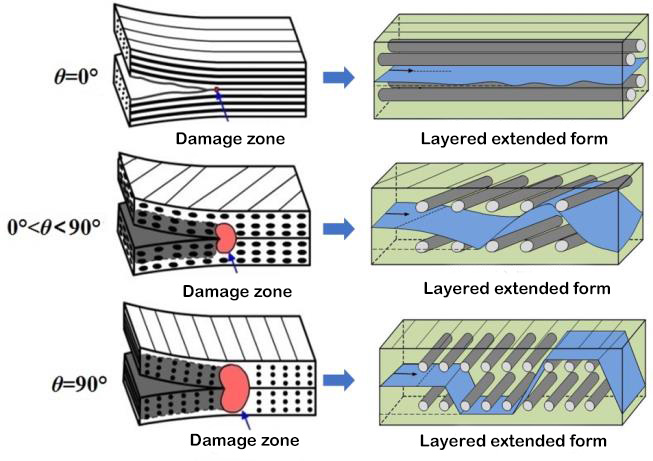
Figura 3 Zona de daño del borde delantero en capas y morfología extendida estratificada^[5]

2. Estudio de simulación numérica

La simulación numérica de la expansión estratificada es un tema de investigación importante en el campo del diseño de estructuras compuestas. Para predecir la falla por delaminación de laminados unidireccionales compuestos, los criterios de expansión estratificada existentes suelen utilizar la tenacidad a la fractura interlaminar constante como parámetro básico de rendimiento.^[10], comparando la tasa de liberación de energía de la punta de la grieta y la tenacidad a la fractura interlaminar. Tamaño para determinar si la estratificación se expande. El mecanismo de falla de los laminados multidireccionales es complejo.^[11,12], que se caracteriza por curvas de resistencia R significativas^[5,13]Los criterios de expansión por capas existentes no consideran esta característica y no son aplicables a la simulación del comportamiento de delaminación de laminados multidireccionales con puentes de fibra. Gong et al.^{[10, 13]}Se mejoraron los criterios de expansión estratificada existentes y se propuso introducir la curva de resistencia R en ellos. Con base en esto, se estableció un criterio de expansión estratificada que considera los efectos del puenteo de fibras. La definición y los parámetros de uso de la unidad cohesiva constitutiva bilineal se estudiaron sistemáticamente mediante métodos numéricos, incluyendo la rigidez inicial de la interfaz, la resistencia de la interfaz, el coeficiente de viscosidad y el número mínimo de elementos en la zona de fuerza cohesiva. Se estableció el modelo de parámetros de la unidad cohesiva correspondiente. Finalmente, se verificó la efectividad y aplicabilidad del criterio de expansión estratificada mejorado y del modelo de parámetros de la unidad cohesiva mediante una prueba de estratificación estática. Sin embargo, los criterios mejorados solo pueden utilizarse para simulaciones estratificadas unidimensionales debido a las dependencias posicionales, y no para extensiones jerárquicas bidimensionales o tridimensionales. Para resolver este problema, el autor propuso además un nuevo constitutivo de fuerza cohesiva trilineal que considera el puenteo de fibras.^[14]La relación constitutiva se ajusta al complejo proceso de expansión en capas desde una perspectiva microscópica y tiene las ventajas de parámetros simples y un significado físico claro.
Además, para simular con precisión el fenómeno de migración estratificada común en el proceso de estratificación de laminados multidireccionales^[11,12], Zhao y otros.^[11,12]Se propuso un modelo de guía de trayectoria de grietas basado en elementos finitos extendidos, que simula un diseño especial. Migración jerárquica en una prueba de estratificación compuesta. Simultáneamente, se propone un modelo de expansión por capas para el comportamiento de expansión en zigzag a lo largo de la interfaz de 90°/90°, que simula con precisión dicho comportamiento.

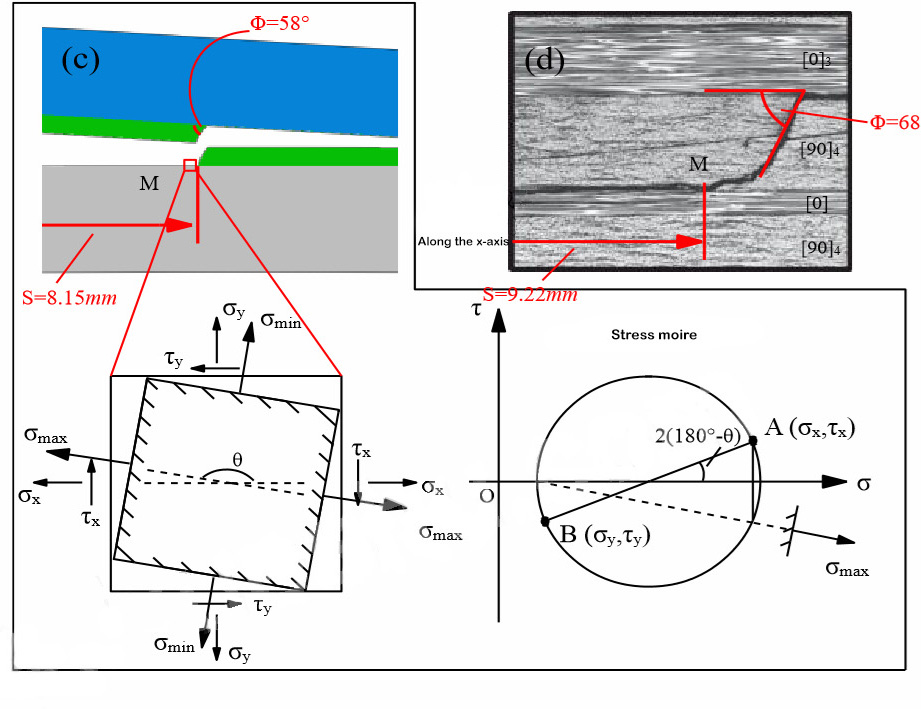Figura 4 Simulación numérica de la migración en capas y resultados experimentales^[15]

Conclusión

Este artículo se centra en los resultados de investigación de este grupo en el campo de la delaminación de laminados compuestos. Los aspectos experimentales incluyen principalmente la influencia del ángulo de laminado de la interfaz y la formación de puentes de fibras en el comportamiento de expansión de la delaminación estática y por fatiga. A través de un gran número de estudios experimentales, se encontró que el mecanismo de falla de laminados multidireccionales de materiales compuestos es complejo. La formación de puentes de fibras es un mecanismo de endurecimiento común de laminados multidireccionales, que es la razón principal de la curva de resistencia R de la tenacidad a la fractura interlaminar. Actualmente, el estudio de la curva de resistencia R bajo la estratificación II es relativamente escaso y requiere mayor investigación. A partir del mecanismo de falla, se propone el modelo de estratificación por fatiga que incluye diversos factores influyentes, que es una dirección de investigación en estratificación por fatiga. En términos de simulación numérica, el grupo de investigación propuso un criterio mejorado de expansión jerárquica y un modelo constitutivo cohesivo para considerar la influencia de la formación de puentes de fibras en el comportamiento de expansión estratificada. Además, se utiliza el elemento finito extendido para simular mejor el fenómeno de migración jerárquica. Este método elimina la necesidad de una división celular fina, eliminando así los problemas asociados con la redivisión de la malla. Presenta ventajas únicas en la simulación de la estratificación de formas arbitrarias, por lo que se requiere mayor investigación en aplicaciones de ingeniería de este método en el futuro.^[16].

Referencias

[1] Y Gong, L Zhao, J Zhang, N Hu. Un nuevo modelo para determinar la resistencia a la delaminación por fatiga en laminados compuestos desde una perspectiva energética. Compos Sci Technol 2018; 167: 489-96.
[2] L Zhao, Y Wang, J Zhang, Y Gong, N Hu, N Li. Modelo basado en XFEM para simular el crecimiento de la delaminación en zigzag en compuestos laminados bajo carga de modo I. Compos Struct 2017; 160: 1155-62.
[3] L Zhao, Y Gong, J Zhang, Y Wang, Z Lu, L Peng, N Hu. Una nueva interpretación del comportamiento de crecimiento de la delaminación por fatiga en laminados multidireccionales de CFRP. Compos Sci Technol 2016; 133: 79-88.
[4] L Peng, J Zhang, L Zhao, R Bao, H Yang, B Fei. Crecimiento de la delaminación en modo I de laminados compuestos multidireccionales bajo carga de fatiga. J Compos Mater 2011; 45: 1077-90.
[5] L Zhao, Y Wang, J Zhang, Y Gong, Z Lu, N Hu, J Xu. Un modelo dependiente de la interfaz de la tenacidad a la fractura de meseta en laminados de CFRP multidireccionales bajo carga de modo I. Composites Part B: Engineering 2017; 131: 196-208.
[6] L Zhao, Y Gong, J Zhang, Y Chen, B Fei. Simulación del crecimiento de la delaminación en laminados multidireccionales bajo cargas de modo I y mixtas de modo I/II utilizando elementos cohesivos. Compos Struct 2014; 116: 509-22.
[7] Y Gong, B Zhang, L Zhao, J Zhang, N Hu, C Zhang. Comportamiento de la curva R de la delaminación de modo mixto I/II en laminados de carbono/epoxi con interfaces unidireccionales y multidireccionales. Compos Struct 2019. (En revisión).
[8] L Peng, J Xu, J Zhang, L Zhao. Crecimiento de la delaminación en modo mixto de laminados compuestos multidireccionales bajo carga de fatiga. Eng Fract Mech 2012; 96: 676-86.
[9] J Zhang, L Peng, L Zhao, B Fei. Tasas y umbrales de crecimiento de la delaminación por fatiga de laminados compuestos sometidos a cargas de modo mixto. Int J Fatigue 2012; 40: 7-15.
[10] Y Gong, L Zhao, J Zhang, Y Wang, N Hu. Criterio de propagación de la delaminación, incluyendo el efecto del puenteo de fibras para la delaminación de modo mixto I/II en laminados multidireccionales de CFRP. Compos Sci Technol 2017; 151: 302-9.
[11] Y Gong, B Zhang, SR Hallett. Migración de delaminación en laminados compuestos multidireccionales bajo carga cuasiestática y de fatiga en modo I. Compos Struct 2018; 189: 160-76.
[12] Y Gong, B Zhang, S Mukhopadhyay, SR Hallett. Estudio experimental sobre la migración de delaminación en laminados multidireccionales bajo carga estática y de fatiga de modo II, en comparación con el modo I. Compos Struct 2018; 201: 683-98.
[13] Y Gong, L Zhao, J Zhang, N Hu. Un criterio de ley de potencia mejorado para la propagación de la delaminación con el efecto de puenteo de fibras a gran escala en laminados multidireccionales compuestos. Compos Struct 2018; 184: 961-8.
[14] Y Gong, Y Hou, L Zhao, W Li, G Yang, J Zhang, N Hu. Un nuevo modelo de zona cohesiva trilineal para el crecimiento de la delaminación en laminados de DCB con el efecto de puenteo de fibras. Compos Struct 2019. (Próximamente).
[15] L Zhao, J Zhi, J Zhang, Z Liu, N Hu. Simulación XFEM de delaminación en laminados compuestos. Composites Part A: Applied Science and Manufacturing 2016; 80: 61-71.
[16] Zhao Libin, Gong Yu, Zhang Jianyu. Avances en la investigación sobre el comportamiento de expansión estratificada de laminados compuestos reforzados con fibra. Revista de Ciencias Aeronáuticas 2019: 1-28.

Fuente:Gong Yu, Wang Yana, Peng Lei, Zhao Libin, Zhang Jianyu. Estudio sobre el comportamiento de expansión estratificada de laminados compuestos avanzados reforzados con fibra de carbono [C]. Conferencia Académica de Mecánica e Ingeniería - Computación Numérica y Análisis de Datos 2019. Sociedad China de Mecánica, Sociedad de Mecánica de Pekín, 2019. a través de ixueshu