යාන්ත්‍ර විද්‍යාව සහ ඉංජිනේරු විද්‍යාව - සංඛ්‍යාත්මක ගණනය කිරීම සහ දත්ත විශ්ලේෂණය
යාන්ත්‍ර විද්‍යාව සහ ඉංජිනේරු විද්‍යාව — සංඛ්‍යාත්මක ගණනය කිරීම් සහ දත්ත විශ්ලේෂණය 2019 අධ්‍යයන සමුළුව, 2019 අප්‍රේල් 19-21, බීජිං
2019 අප්‍රේල් 19-21, බීජිං, චීනය
උසස් කාබන් ෆයිබර් ශක්තිමත් කරන ලද සංයුක්ත ලැමිෙන්ට් පත්‍රයේ ස්ථර ප්‍රසාරණ හැසිරීම පිළිබඳ අධ්‍යයනය
ගොං යූ1 යි*, වැන්ග් යනා2, Peng Lei3 යි, Zhao Libin4, Zhang Jianyu1 යි
1 යිචොංකිං විශ්ව විද්‍යාලය, චොංකිං, 400044, චීනය
2චීන ගුවන් සේවා පර්යේෂණ ආයතනය බීජිං ගුවන් යානා ද්‍රව්‍ය පර්යේෂණ ආයතනය, බීජිං, 100095, චීනය
3 යිචීන වාණිජ ගුවන් යානා බීජිං සිවිල් ගුවන් යානා තාක්ෂණ පර්යේෂණ මධ්‍යස්ථානය, බීජිං, 102211, චීනය
4බීජිං ගුවන් හා අභ්‍යවකාශ විද්‍යා විශ්ව විද්‍යාලය, බීජිං, 100191, චීනය
වියුක්තලැමිෙන්ට් ව්‍යුහය සංයුක්ත සඳහා බහුලව භාවිතා වන සංයුක්ත වින්‍යාසයන්ගෙන් එකකි, නමුත් දුර්වල අන්තර්ලැමිනර් ගුණාංග හේතුවෙන් ඩිලමිනේෂන් එහි ප්‍රධාන අසාර්ථක මාදිලිය බවට පත්වේ. ඉංජිනේරු භාවිතයේදී බහුලව භාවිතා වන බහු-ස්ථර ලැමිෙන්ට් ස්ථරීකරණය සහ ප්‍රසාරණ හැසිරීම පිළිබඳ පර්යේෂණ සෑම විටම විද්වතුන් සඳහා උණුසුම් මාතෘකාවක් වී ඇත. මෙම පත්‍රිකාවේ, චොංකිං විශ්ව විද්‍යාලයේ සහ බීජිං ගුවන් විද්‍යා හා තාරකා විද්‍යා විශ්ව විද්‍යාලයේ තෙහෙට්ටුව අස්ථි බිඳීමේ රසායනාගාරයේ කාබන් ෆයිබර් ශක්තිමත් කරන ලද සංයුක්ත ඩිලමිනේෂන් පිළිබඳ පර්යේෂණ ප්‍රතිඵල පර්යේෂණාත්මක පර්යේෂණ සහ සංඛ්‍යාත්මක අනුකරණයේ අංශ දෙකකින් හඳුන්වා දී ඇත. අවසාන වශයෙන්, ක්ෂේත්‍රයේ සංවර්ධන දිශාව අපේක්ෂා කෙරේ.
මූල පද:කාබන් ෆයිබර් ශක්තිමත් කරන ලද සංයුක්ත, ලැමිෙන්ට්, ඩිලමිනේෂන්, තෙහෙට්ටුව ස්ථරීකරණය
හැඳින්වීම
සංයුක්ත ද්‍රව්‍යවලට ඉහළ නිශ්චිත ශක්තියක් සහ ඉහළ නිශ්චිත තද බවක් වැනි විශිෂ්ට ගුණාංග ඇති අතර, අභ්‍යවකාශ, බලශක්ති තාක්‍ෂණය සහ සිවිල් ප්‍රවාහනය සහ ඉදිකිරීම් සඳහා බහුලව භාවිතා වේ. සංයුක්ත ද්‍රව්‍ය සැකසීම සහ භාවිතා කිරීම අතරතුර, තන්තු සහ අනුකෘතිය බර යටතේ විවිධ මට්ටමේ හානිවලට භාජනය වේ. සංයුක්ත ලැමිෙන්ට් සඳහා පොදු අසාර්ථක ක්‍රම අතර අන්තර් ස්ථර හානි සහ ස්ථර තුළ හානි ඇතුළත් වේ. ඝණකම දිශාවට ශක්තිමත් කිරීමක් නොමැතිකම නිසා, ලැමිෙන්ට් වල පාර්ශ්වීය යාන්ත්‍රික ගුණාංග දුර්වල වන අතර, බාහිර බලපෑම් බර යටතේ විච්ඡේදක හානි සිදුවීමට බොහෝ දුරට ඉඩ ඇත. ස්ථරීකරණය වූ හානිය සිදුවීම සහ ප්‍රසාරණය වීම ව්‍යුහාත්මක දෘඪතාව සහ ශක්තිය අඩුවීමට හේතු වන අතර, ව්‍යසනකාරී අනතුරු පවා ඇති කරයි.[1-3]. එබැවින්, සංයුක්ත ද්‍රව්‍යවල ව්‍යුහාත්මක සැලසුම් සහ ශක්තිය විශ්ලේෂණය මගින් විරූපණ ගැටළුව වඩ වඩාත් සැලකිලිමත් වන අතර, සංයුක්ත ද්‍රව්‍යවල ස්ථර ප්‍රසාරණ හැසිරීම අධ්‍යයනය කිරීම අවශ්‍ය වේ.[4].
ලැමිෙන්ට් වල ස්ථර ප්‍රසාරණ හැසිරීම පිළිබඳ පර්යේෂණ
1. පර්යේෂණාත්මක අධ්‍යයනය
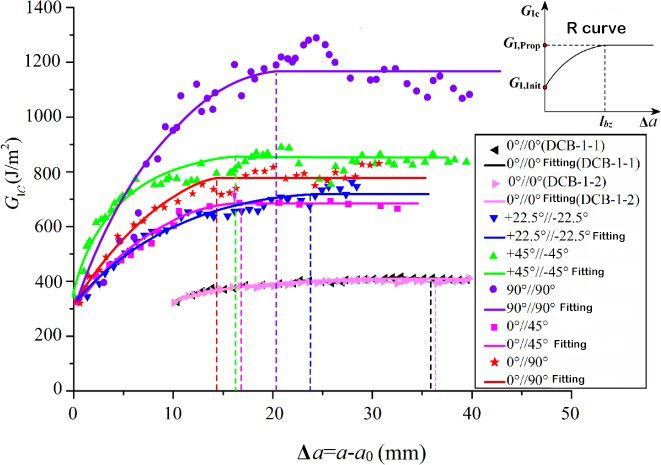
සංයුක්ත ස්ථර අතර යාන්ත්‍රික ගුණාංගවල ලාක්ෂණික පරාමිතිය වන්නේ අන්තර්ලැමිනර් අස්ථි බිඳීමේ තද බවයි. I වර්ගය, II වර්ගය සහ I/II දෙමුහුන් ඒක දිශානුගත ලැමිෙන්ට් වල අන්තර්ලැමිනර් අස්ථි බිඳීමේ තද බව තීරණය කිරීම සඳහා අනුරූප පරීක්ෂණ ප්‍රමිතීන් ස්ථාපිත කර ඇත. අනුරූප පරීක්ෂණ උපකරණය රූපය 1 හි දක්වා ඇත. කෙසේ වෙතත්, සංයුක්ත ද්‍රව්‍යවල බහු දිශානුගත ලැමිෙන්ට් බොහෝ විට සැබෑ ඉංජිනේරු ව්‍යුහය තුළ භාවිතා වේ. එබැවින්, බහු දිශානුගත ලැමිෙන්ට් වල ස්ථරීකරණය සහ ප්‍රසාරණ හැසිරීම පිළිබඳ පර්යේෂණාත්මක අධ්‍යයනයට වඩා වැදගත් න්‍යායාත්මක වැදගත්කමක් සහ ඉංජිනේරු වටිනාකමක් ඇත. බහු ස්ථර ලැමිෙන්ට් ස්ථර ආරම්භය සහ ප්‍රසාරණය අත්තනෝමතික ස්ථර කෝණ සහිත අතුරුමුහුණත් අතර සිදුවන අතර, ස්ථර ප්‍රසාරණ හැසිරීම ඒක දිශානුගත ලැමිෙන්ට් වලට වඩා සැලකිය යුතු ලෙස වෙනස් වන අතර, ප්‍රසාරණ යාන්ත්‍රණය වඩාත් සංකීර්ණ වේ. පර්යේෂකයන්ට බහු දිශානුගත ලැමිෙන්ට් පිළිබඳ සාපේක්ෂව ස්වල්ප පර්යේෂණාත්මක අධ්‍යයනයන් ඇති අතර, අන්තර්ලැමිනර් අස්ථි බිඳීමේ තද බව තීරණය කිරීම තවමත් ජාත්‍යන්තර ප්‍රමිතියක් ස්ථාපිත කර නොමැත. පර්යේෂණ කණ්ඩායම විවිධ අතුරුමුහුණත් සැකැස්ම කෝණ සහිත සංයුක්ත ලැමිෙන්ට් නිර්මාණය කිරීම සඳහා T700 සහ T800 කාබන් ෆයිබර් භාවිතා කළ අතර, ස්ථිතික සහ තෙහෙට්ටුව ඉවත් කිරීමේ හැසිරීම් මත අතුරුමුහුණත් සැකැස්ම කෝණය සහ තන්තු පාලම්වල බලපෑම අධ්‍යයනය කළේය. ස්ථරයේ පසුපස දාරයෙන් සාදන ලද තන්තු පාලම අන්තර්ලැමිනර් අස්ථි බිඳීමේ දෘඪතාවට විශාල බලපෑමක් ඇති කරන බව සොයාගෙන ඇත. ස්ථරීකරණය ප්‍රසාරණය වන විට, අන්තර්ලැමිනර් අස්ථි බිඳීමේ දෘඪතාව අඩු ආරම්භක අගයකින් ක්‍රමයෙන් වැඩි වන අතර, ස්ථරීකරණය යම් දිගකට ළඟා වූ විට, එය ස්ථාවර අගයකට ළඟා වේ, එනම් R ප්‍රතිරෝධක වක්‍ර සංසිද්ධිය. අන්තර් ස්ථරයේ ආරම්භක අස්ථි බිඳීමේ දෘඪතාව දුම්මලයේ අස්ථි බිඳීමේ දෘඪතාවට ආසන්න වශයෙන් සමාන වන අතර ආසන්න වශයෙන් සමාන වේ, එය අනුකෘතියේම අස්ථි බිඳීමේ දෘඪතාව මත රඳා පවතී.[5, 6]. කෙසේ වෙතත්, විවිධ අතුරුමුහුණත් වල අන්තර්ලැමිනර් අස්ථි බිඳීමේ දෘඪතාව දිගු කිරීමේ අගයන් බෙහෙවින් වෙනස් වේ. සැලකිය යුතු අතුරුමුහුණත් ස්ථර කෝණ යැපීම ඉදිරිපත් කෙරේ. මෙම යැපීමට ප්‍රතිචාර වශයෙන්, ෂාඕ සහ වෙනත් අය.[5]ස්ථරීකෘත ප්‍රතිරෝධක ප්‍රභවයේ භෞතික යාන්ත්‍රණය මත පදනම්ව, අන්තර්ලැමිනර් අස්ථි බිඳීමේ දෘඪතා ස්ථායිතා අගය කොටස් දෙකකින් සමන්විත බව සැලකේ, එක් කොටසක් අසම්බන්ධිත ස්ථර අතුරුමුහුණතේ අස්ථි බිඳීමේ කාර්යය වන අතර අනෙක් කොටස අභ්‍යන්තර ස්ථර හානිය සහ තන්තු වේ. පාලම් කිරීම නිසා ඇතිවන අස්ථි බිඳීමේ කාර්යය. ස්ථර ඉදිරිපස ආතති ඉදිරිපස ක්ෂේත්‍රයේ සීමිත මූලද්‍රව්‍ය විශ්ලේෂණය හරහා, අස්ථි බිඳීමේ කාර්යයේ දෙවන කොටස ඩිලමිනේෂන් ඉදිරිපස හානි කලාපයේ ගැඹුර මත රඳා පවතින බව සොයාගෙන ඇත (රූපය 3 හි පෙන්වා ඇති පරිදි), සහ හානි කලාපයේ ගැඹුර අතුරු මුහුණත පිරිසැලසුම් කෝණයට සමානුපාතික වේ. අතුරුමුහුණත් ස්ථර කෝණයේ සයිනොසොයිඩල් ශ්‍රිතය මගින් ප්‍රකාශිත I-වර්ගයේ අස්ථි බිඳීමේ දෘඪතා ස්ථායිතා අගය පිළිබඳ න්‍යායාත්මක ආකෘතියක් ඉදිරිපත් කෙරේ.
ගොං සහ තවත් අය.[7]විවිධ මිශ්‍ර කිරීමේ අනුපාත යටතේ I/II දෙමුහුන් ස්ථරීකරණ පරීක්ෂණය සිදු කරන ලද අතර, ලැමිෙන්ට් වල I/II දෙමුහුන් ස්ථරීකරණයට සැලකිය යුතු R ප්‍රතිරෝධක වක්‍ර ලක්ෂණ ඇති බව සොයා ගන්නා ලදී. විවිධ පරීක්ෂණ කොටස් අතර අස්ථි බිඳීමේ දෘඪතාව විශ්ලේෂණය කිරීමෙන්, මිශ්‍ර කිරීමේ අනුපාතය වැඩි වීමත් සමඟ පරීක්ෂණ කැබැල්ලේ අන්තර්ලැමිනර් අස්ථි බිඳීමේ දෘඪතාවයේ ආරම්භක අගය සහ ස්ථායී අගය සැලකිය යුතු ලෙස වැඩි වන බව සොයා ගන්නා ලදී. ඊට අමතරව, විවිධ මිශ්‍ර කිරීමේ අනුපාත යටතේ අන්තර් ස්ථරයේ ආරම්භක සහ ස්ථායී අස්ථි බිඳීමේ දෘඪතාව BK නිර්ණායකය මගින් විස්තර කළ හැකිය.
තෙහෙට්ටුව ස්ථරීකරණය සම්බන්ධයෙන්, පරීක්ෂණය අතරතුර සැලකිය යුතු තන්තු පාලමක් ද නිරීක්ෂණය විය. පරීක්ෂණ දත්ත විශ්ලේෂණය හරහා, සංයුක්ත ද්‍රව්‍යයේ තෙහෙට්ටුව විරූපණ ප්‍රසාරණය "ප්‍රතිරෝධක වක්‍රය" මගින් බලපාන බව සොයාගෙන ඇත, එබැවින් සාම්ප්‍රදායික තෙහෙට්ටුව ස්ථරීකරණ ප්‍රසාරණ අනුපාත ආකෘතිය සහ එළිපත්ත අගය තවදුරටත් අදාළ නොවේ. න්‍යායාත්මක විශ්ලේෂණයේ පදනම මත, ෂැං සහ පෙන්ග්[4,8,9]සංයුක්ත ද්‍රව්‍යවල තෙහෙට්ටුව විරූපණ ප්‍රසාරණය සඳහා අවශ්‍ය ශක්තිය ප්‍රකාශ කිරීම සඳහා තෙහෙට්ටුව විරූපණ ප්‍රසාරණ ප්‍රතිරෝධය හඳුන්වා දුන් අතර, සාමාන්‍යකරණය කළ වික්‍රියා ශක්තිය තවදුරටත් යෝජනා කළේය. මුදා හැරීමේ අනුපාතය යනු තෙහෙට්ටුව ස්ථරීකරණය වූ ප්‍රසාරණ අනුපාත ආකෘතිය සහ පාලන පරාමිතීන්ගේ එළිපත්ත අගයයි. ආකෘතියේ සහ සාමාන්‍යකරණය කළ එළිපත්ත පරාමිතියේ අදාළත්වය අත්හදා බැලීම් මගින් සත්‍යාපනය කෙරේ. තවද, ෂාඕ සහ වෙනත් අය.[3]තන්තු පාලම, ආතති අනුපාතය සහ බර-මිශ්‍ර කිරීමේ අනුපාතය තෙහෙට්ටුව ස්ථරීකරණය සහ ප්‍රසාරණ හැසිරීම කෙරෙහි ඇති කරන බලපෑම් පුළුල් ලෙස සලකා බැලූ අතර, ආතති අනුපාතයේ බලපෑම සැලකිල්ලට ගනිමින් සාමාන්‍යකරණය කළ තෙහෙට්ටුව ස්ථරීකරණය වූ ප්‍රසාරණ අනුපාත ආකෘතියක් ස්ථාපිත කරන ලදී. විවිධ ආතති අනුපාත සහ මිශ්‍ර කිරීමේ අනුපාත සහිත තෙහෙට්ටුව ස්ථරීකරණය කිරීමේ පරීක්ෂණ මගින් ආකෘතියේ නිරවද්‍යතාවය සත්‍යාපනය කරන ලදී. සාමාන්‍යකරණය කළ තෙහෙට්ටුව ස්ථරීකරණය වූ ප්‍රසාරණ අනුපාත ආකෘතියේ තෙහෙට්ටුව ස්ථරීකරණය වූ ප්‍රසාරණ ප්‍රතිරෝධයේ භෞතික ප්‍රමාණය සඳහා, ගොං සහ වෙනත් අය.[1]අත්හදා බැලීම් හරහා සීමිත විවික්ත දත්ත ලක්ෂ්‍ය පමණක් ලබා ගත හැකි ගණනය කිරීමේ ක්‍රමයේ දුර්වලතාවය ජය ගැනීමට සහ ශක්ති දෘෂ්ටි කෝණයෙන් තෙහෙට්ටුව ස්ථාපිත කිරීමට. ස්ථරීකෘත විස්තීර්ණ ප්‍රතිරෝධය ගණනය කිරීම සඳහා විශ්ලේෂණාත්මක ආකෘතියක්. ආකෘතියට තෙහෙට්ටුව ස්ථරීභවනය සහ ප්‍රසාරණ ප්‍රතිරෝධයේ ප්‍රමාණාත්මක නිර්ණය සාක්ෂාත් කර ගත හැකි අතර, යෝජිත සාමාන්‍යකරණය කරන ලද තෙහෙට්ටුව ස්ථරීභවනය වූ ප්‍රසාරණ අනුපාත ආකෘතියේ යෙදීම සඳහා න්‍යායාත්මක සහාය ලබා දිය හැකිය.
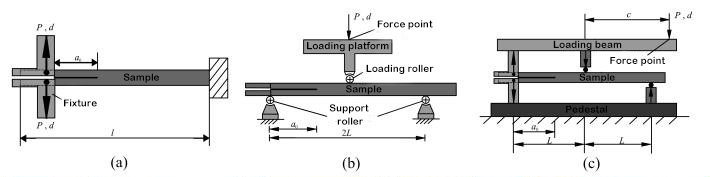රූපය 1 ස්ථරීකෘත පරීක්ෂණ උපාංග රූප සටහන
රූපය 2 අන්තර්-ස්ථර අස්ථි බිඳීමේ දෘඪතාව R ප්‍රතිරෝධක වක්‍රය[5]
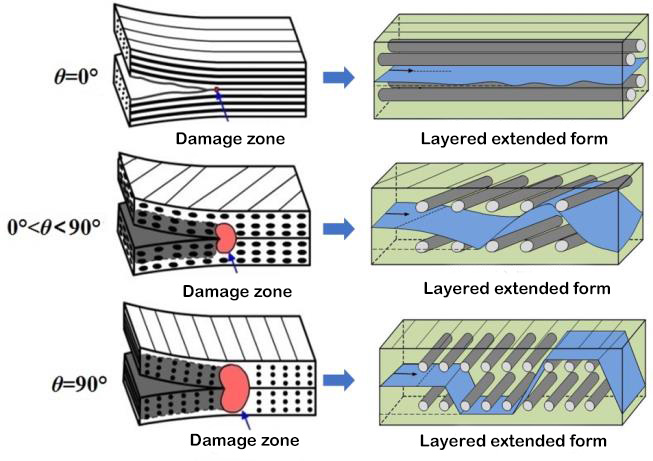
රූපය 3 ස්ථර ප්‍රමුඛ දාර හානි කලාපය සහ ස්ථරීකෘත විස්තීර්ණ රූප විද්‍යාව[5]
2. සංඛ්‍යාත්මක සමාකරණ අධ්‍යයනය
ස්ථර ප්‍රසාරණයේ සංඛ්‍යාත්මක අනුකරණය සංයුක්ත ව්‍යුහ සැලසුම් ක්ෂේත්‍රයේ වැදගත් පර්යේෂණ අන්තර්ගතයකි. සංයුක්ත ඒක දිශානුගත ලැමිෙන්ට් වල ඩිලමිනේෂන් අසාර්ථකත්වය පුරෝකථනය කිරීමේදී, පවතින ස්ථරීකරණ ප්‍රසාරණ නිර්ණායක සාමාන්‍යයෙන් මූලික කාර්ය සාධන පරාමිතිය ලෙස නියත අන්තර් ලැමිනර් අස්ථි බිඳීමේ තද බව භාවිතා කරයි.[10], ඉරිතැලීම් තුඩ ශක්ති මුදා හැරීමේ අනුපාතය සහ අන්තර්ලැමිනර් අස්ථි බිඳීමේ තද බව සංසන්දනය කිරීමෙන්. ස්ථර කිරීම ප්‍රසාරණය වන්නේද යන්න තීරණය කිරීමට ප්‍රමාණය. බහු දිශානුගත ලැමිෙන්ට් වල අසාර්ථක යාන්ත්‍රණය සංකීර්ණ වේ.[11,12], එය සැලකිය යුතු R ප්‍රතිරෝධක වක්‍ර මගින් සංලක්ෂිත වේ[5,13]. පවතින ස්ථර ප්‍රසාරණ නිර්ණායක මෙම ලක්ෂණය සැලකිල්ලට නොගන්නා අතර තන්තු අඩංගු පාලම් බහු දිශානුගත ලැමිෙන්ට් වල විරූපණ හැසිරීම අනුකරණය කිරීමට අදාළ නොවේ. ගොං සහ වෙනත් අය.[10, 13]පවතින ස්ථරීකෘත ප්‍රසාරණ නිර්ණායක වැඩිදියුණු කර R ප්‍රතිරෝධක වක්‍රය නිර්ණායකවලට හඳුන්වා දීමට යෝජනා කළ අතර, මේ මත පදනම්ව, තන්තු පාලමේ බලපෑම් සලකා බලා ස්ථරීකෘත ප්‍රසාරණ නිර්ණායකයක් ස්ථාපිත කරන ලදී. ද්වි රේඛීය ව්‍යුහාත්මක ඒකාබද්ධ ඒකකයේ නිර්වචනය සහ භාවිත පරාමිතීන් සංඛ්‍යාත්මක ක්‍රම මගින් ක්‍රමානුකූලව අධ්‍යයනය කරන ලදී, ආරම්භක අතුරුමුහුණත් තද බව, අතුරුමුහුණත් ශක්තිය, දුස්ස්රාවීතා සංගුණකය සහ ඒකාබද්ධ බල කලාපයේ අවම මූලද්‍රව්‍ය ගණන ඇතුළුව. අනුරූප ඒකාබද්ධ ඒකක පරාමිති ආකෘතිය ස්ථාපිත කරන ලදී. අවසාන වශයෙන්, වැඩිදියුණු කළ ස්ථර ප්‍රසාරණ නිර්ණායකයේ සහ ඒකාබද්ධ ඒකක පරාමිති ආකෘතියේ කාර්යක්ෂමතාව සහ අදාළත්වය ස්ථිතික ස්ථරීකරණ පරීක්ෂණය මගින් සත්‍යාපනය කෙරේ. කෙසේ වෙතත්, වැඩිදියුණු කළ නිර්ණායක භාවිතා කළ හැක්කේ ස්ථානීය පරායත්තතා හේතුවෙන් ඒක-මාන ස්ථර සමාකරණ සඳහා පමණක් වන අතර ද්වි-හෝ ත්‍රි-මාන ධූරාවලි දිගු සඳහා නොවේ. මෙම ගැටළුව විසඳීම සඳහා, කතුවරයා තන්තු පාලම සලකා බලා නව ත්‍රි-රේඛීය ඒකාබද්ධ බල ව්‍යුහාත්මක එකක් තවදුරටත් යෝජනා කළේය.[14]. ව්‍යුහාත්මක සම්බන්ධතාවය ක්ෂුද්‍ර දෘෂ්ටිකෝණයකින් ස්ථර ප්‍රසාරණය වීමේ සංකීර්ණ ක්‍රියාවලියට ගැලපෙන අතර සරල පරාමිතීන් සහ පැහැදිලි භෞතික අර්ථයේ වාසි ඇත.
ඊට අමතරව, බහු දිශානුගත ලැමිෙන්ට් වල ස්ථරීකරණ ක්‍රියාවලියේදී බහුලව දක්නට ලැබෙන ස්ථරීකරණ සංක්‍රමණ සංසිද්ධිය නිවැරදිව අනුකරණය කිරීම සඳහා[11,12], ෂාඕ සහ තවත් අය.[11,12]විශේෂ සැලසුමක් අනුකරණය කරමින් විස්තීරණ සීමිත මූලද්‍රව්‍යයක් මත පදනම් වූ ඉරිතැලීම් මාර්ග මාර්ගෝපදේශ ආකෘතියක් යෝජනා කළේය. සංයුක්ත ස්ථරීකරණ පරීක්ෂණයක ධූරාවලි සංක්‍රමණය. ඒ සමඟම, 90°/90° ස්ථර අතුරුමුහුණත දිගේ සිග්සැග් ස්ථර ප්‍රසාරණ හැසිරීම සඳහා ස්ථර ප්‍රසාරණ ආකෘතියක් යෝජනා කර ඇති අතර, එය 90°/90° අතුරුමුහුණතේ ස්ථර ප්‍රසාරණ හැසිරීම නිවැරදිව අනුකරණය කරයි.
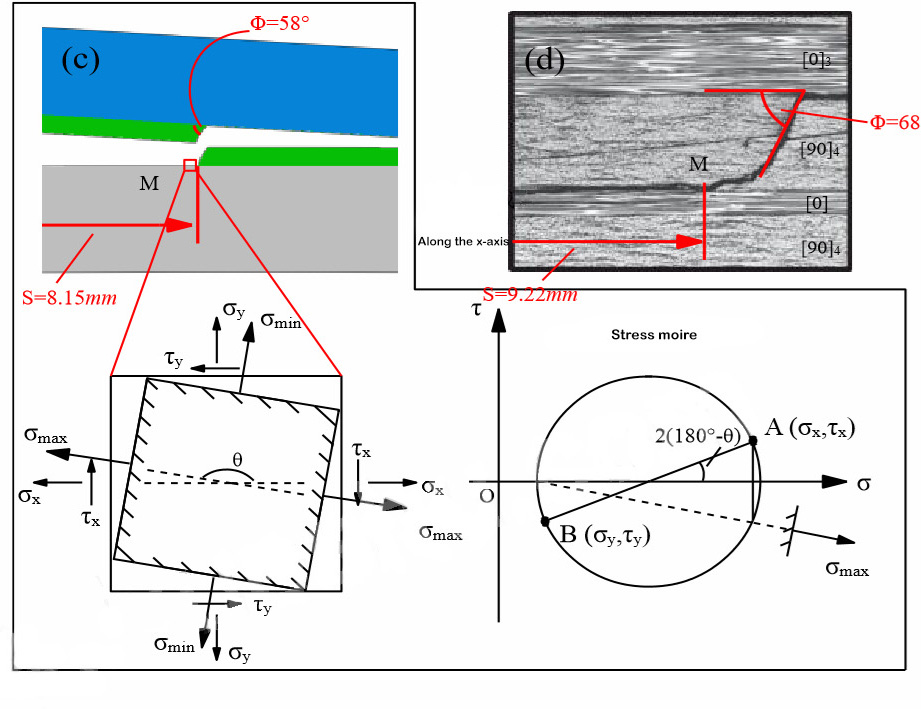රූපය 4 ස්ථර සංක්‍රමණයේ සංඛ්‍යාත්මක අනුකරණය සහ පර්යේෂණාත්මක ප්‍රතිඵල[15]
නිගමනය
මෙම පත්‍රිකාව සංයුක්ත ලැමිෙන්ට් විරූපණ ක්ෂේත්‍රයේ මෙම කණ්ඩායමේ පර්යේෂණ ප්‍රතිඵල කෙරෙහි අවධානය යොමු කරයි. පර්යේෂණාත්මක අංශවලට ප්‍රධාන වශයෙන් ස්ථිතික සහ තෙහෙට්ටුව විරූපණ ප්‍රසාරණ හැසිරීම් කෙරෙහි අතුරුමුහුණත් සැකැස්මේ කෝණය සහ තන්තු පාලමේ බලපෑම ඇතුළත් වේ. පර්යේෂණාත්මක අධ්‍යයන විශාල සංඛ්‍යාවක් හරහා, සංයුක්ත ද්‍රව්‍යවල බහු-දිශානුගත ලැමිෙන්ට් අසාර්ථක යාන්ත්‍රණය සංකීර්ණ බව සොයාගෙන ඇත. තන්තු පාලම යනු බහු-දිශානුගත ලැමිෙන්ට් වල පොදු දැඩි කිරීමේ යාන්ත්‍රණයක් වන අතර එය අන්තර්-ලැමිනර් අස්ථි බිඳීමේ දෘඩතාවයේ R-ප්‍රතිරෝධක වක්‍රයට ප්‍රධාන හේතුවයි. වර්තමානයේ, II ස්ථරීකරණය යටතේ R ප්‍රතිරෝධක වක්‍ර අධ්‍යයනය සාපේක්ෂව අඩු වන අතර වැඩිදුර පර්යේෂණ අවශ්‍ය වේ. අසාර්ථක යාන්ත්‍රණයෙන් පටන් ගෙන, විවිධ බලපෑම් කරන සාධක ඇතුළුව තෙහෙට්ටුව ස්ථරීකරණ ආකෘතිය යෝජනා කරනු ලැබේ, එය තෙහෙට්ටුව ස්ථරීකරණ පර්යේෂණයේ දිශාවකි. සංඛ්‍යාත්මක සමාකරණය සම්බන්ධයෙන් ගත් කල, පර්යේෂණ කණ්ඩායම ස්ථරීකරණය වූ ප්‍රසාරණ හැසිරීම් කෙරෙහි තන්තු පාලමේ බලපෑම සලකා බැලීම සඳහා වැඩිදියුණු කළ ධූරාවලි ප්‍රසාරණ නිර්ණායකයක් සහ ඒකාබද්ධ ව්‍යුහාත්මක ආකෘතියක් යෝජනා කළේය. ඊට අමතරව, ධූරාවලි සංක්‍රමණ සංසිද්ධිය වඩා හොඳින් අනුකරණය කිරීම සඳහා විස්තීර්ණ සීමිත මූලද්‍රව්‍යය භාවිතා කරයි. මෙම ක්‍රමය සියුම් සෛල බෙදීමේ අවශ්‍යතාවය ඉවත් කරයි, දැල් නැවත බෙදීම හා සම්බන්ධ ගැටළු ඉවත් කරයි. අත්තනෝමතික හැඩතලවල ස්ථරීකරණය අනුකරණය කිරීමේදී එයට අද්විතීය වාසි ඇති අතර, අනාගතයේදී මෙම ක්‍රමය පිළිබඳ තවත් ඉංජිනේරු යෙදුම් පර්යේෂණ අවශ්‍ය වේ.[16].
ආශ්රිත
[1] Y Gong, L Zhao, J Zhang, N Hu. ශක්ති දෘෂ්ටි කෝණයකින් සංයුක්ත ලැමිෙන්ට් වල තෙහෙට්ටුව ඉවත් කිරීමේ ප්‍රතිරෝධය තීරණය කිරීම සඳහා නව ආකෘතියක්. Compos Sci Technol 2018; 167: 489-96.
[2] L Zhao, Y Wang, J Zhang, Y Gong, N Hu, N Li. මාදිලිය I පැටවීම යටතේ ලැමිෙන්ටඩ් සංයුක්තවල සිග්සැග් ඩිලමිනේෂන් වර්ධනය අනුකරණය කිරීම සඳහා XFEM-පාදක ආකෘතිය. Compos Struct 2017; 160: 1155-62.
[3] L Zhao, Y Gong, J Zhang, Y Wang, Z Lu, L Peng, N Hu. CFRP බහු දිශානුගත ලැමිෙන්ට් වල තෙහෙට්ටුව ඉවත් කිරීමේ වර්ධන හැසිරීම පිළිබඳ නව අර්ථකථනයක්. Compos Sci Technol 2016; 133: 79-88.
[4] එල් පෙන්, ජේ ෂැං, එල් ෂාඕ, ආර් බාඕ, එච් යැං, බී ෆෙයි. තෙහෙට්ටුව පැටවීම යටතේ බහු දිශානුගත සංයුක්ත ලැමිෙන්ට් වල ප්‍රකාරය I ඩිලමිනේෂන් වර්ධනය. ජේ කොම්පෝස් මේටර් 2011; 45: 1077-90.
[5] L Zhao, Y Wang, J Zhang, Y Gong, Z Lu, N Hu, J Xu. මාදිලිය I පැටවීම යටතේ බහු දිශානුගත CFRP ලැමිෙන්ට් වල සානුව අස්ථි බිඳීමේ දෘඪතාව පිළිබඳ අතුරු මුහුණත මත රඳා පවතින ආකෘතියකි. සංයුක්ත B කොටස: ඉංජිනේරු විද්‍යාව 2017; 131: 196-208.
[6] L Zhao, Y Gong, J Zhang, Y Chen, B Fei. සංයුක්ත මූලද්‍රව්‍ය භාවිතා කරමින් මාදිලිය I සහ මිශ්‍ර මාදිලිය I/II පැටවීම් යටතේ බහු දිශානුගත ලැමිෙන්ට් වල ඩිලමිනේෂන් වර්ධනය අනුකරණය කිරීම. Compos Struct 2014; 116: 509-22.
[7] Y Gong, B Zhang, L Zhao, J Zhang, N Hu, C Zhang. ඒක දිශානුගත සහ බහු දිශානුගත අතුරුමුහුණත් සහිත කාබන්/ඉෙපොක්සි ලැමිෙන්ට් වල මිශ්‍ර-මාදිලියේ I/II විරූපණයේ R-වක්‍ර හැසිරීම. Compos Struct 2019. (සමාලෝචනය යටතේ).
[8] එල් පෙන්, ජේ ෂු, ජේ ෂැං, එල් ෂාඕ. තෙහෙට්ටුව පැටවීම යටතේ බහු දිශානුගත සංයුක්ත ලැමිෙන්ට් වල මිශ්‍ර මාදිලියේ ඩිලමිනේෂන් වර්ධනය. ඉංග්‍රීසි ෆ්‍රැක්ට් මෙක් 2012; 96: 676-86.
[9] J Zhang, L Peng, L Zhao, B Fei. මිශ්‍ර මාදිලියේ පැටවීම යටතේ සංයුක්ත ලැමිෙන්ට් වල තෙහෙට්ටුව ඉවත් කිරීමේ වර්ධන අනුපාත සහ සීමාවන්. Int J Fatigue 2012; 40: 7-15.
[10] Y Gong, L Zhao, J Zhang, Y Wang, N Hu. CFRP බහු දිශානුගත ලැමිෙන්ට් වල මිශ්‍ර-මාදිලියේ I/II ඩිලමිනේෂන් සඳහා තන්තු පාලමේ බලපෑම ඇතුළුව ඩිලමිනේෂන් ප්‍රචාරණ නිර්ණායකය. Compos Sci Technol 2017; 151: 302-9.
[11] Y Gong, B Zhang, SR Hallett. මාදිලිය I අර්ධ-ස්ථිතික සහ තෙහෙට්ටුව පැටවීම යටතේ බහු දිශානුගත සංයුක්ත ලැමිෙන්ට් වල ඩිලමිනේෂන් සංක්‍රමණය. Compos Struct 2018; 189: 160-76.
[12] Y Gong, B Zhang, S Mukhopadhyay, SR Hallett. මාදිලිය I හා සැසඳීමේදී, මාදිලිය II ස්ථිතික සහ තෙහෙට්ටුව පැටවීම යටතේ බහු දිශානුගත ලැමිෙන්ට් වල ඩිලමිනේෂන් සංක්‍රමණය පිළිබඳ පර්යේෂණාත්මක අධ්‍යයනය. Compos Struct 2018; 201: 683-98.
[13] Y Gong, L Zhao, J Zhang, N Hu. සංයුක්ත බහු දිශානුගත ලැමිෙන්ට් වල මහා පරිමාණ තන්තු පාලම්වල බලපෑම සහිත delamination ප්‍රචාරණය සඳහා වැඩිදියුණු කළ බල නීති නිර්ණායකයකි. Compos Struct 2018; 184: 961-8.
[14] වයි ගොං, වයි හූ, එල් ෂාඕ, ඩබ්ලිව් ලී, ජී යැං, ජේ ෂැං, එන් හූ. ෆයිබර් බ්‍රිජිං ආචරණය සහිත ඩීසීබී ලැමිෙන්ට් වල ඩිලමිනේෂන් වර්ධනය සඳහා නව ත්‍රි-රේඛීය ඒකාබද්ධ කලාප ආකෘතියක්. සංයුක්ත ව්‍යුහය 2019. (ඉදිරිපත් කිරීමට ඇත)
[15] L Zhao, J Zhi, J Zhang, Z Liu, N Hu. සංයුක්ත ලැමිෙන්ට් වල ඩිලමිනේෂන් XFEM සමාකරණය. සංයුක්ත A කොටස: ව්‍යවහාරික විද්‍යාව සහ නිෂ්පාදනය 2016; 80: 61-71.
[16] ෂාඕ ලිබින්, ගොං යූ, ෂැං ජියැන්යු. තන්තු ශක්තිමත් කරන ලද සංයුක්ත ලැමිෙන්ට් වල ස්ථරීකෘත ප්‍රසාරණ හැසිරීම පිළිබඳ පර්යේෂණ ප්‍රගතිය. ගුවන් යානා විද්‍යා සඟරාව 2019: 1-28.
මූලාශ්‍රය:ගොං යූ, වැන්ග් යනා, පෙන්ග් ලී, ෂාඕ ලිබින්, ෂැං ජියැන්යු. උසස් කාබන් ෆයිබර් ශක්තිමත් කරන ලද සංයුක්ත ලැමිෙන්ට් වල ස්ථරීකෘත ප්‍රසාරණ හැසිරීම පිළිබඳ අධ්‍යයනය[C]. යාන්ත්‍ර විද්‍යාව සහ ඉංජිනේරු විද්‍යාව - සංඛ්‍යාත්මක ගණනය කිරීම් සහ දත්ත විශ්ලේෂණය 2019 අධ්‍යයන සමුළුව. චීන යාන්ත්‍රික සංගමය, බීජිං යාන්ත්‍රික සංගමය, 2019. හරහා ඉක්සුෂු
පළ කළ කාලය: නොවැම්බර්-15-2019