ნახშირბადის ბოჭკოვანი გამაგრებული კომპოზიტური ლამინატის ფურცლის ფენოვანი გაფართოების ქცევის შესწავლა

მექანიკა და ინჟინერია - რიცხვითი გამოთვლები და მონაცემთა ანალიზი
მექანიკა და ინჟინერია — რიცხვითი გამოთვლები და მონაცემთა ანალიზი 2019 წლის აკადემიური კონფერენცია, 2019 წლის 19-21 აპრილი, პეკინი
2019 წლის 19-21 აპრილი, პეკინი, ჩინეთი

ნახშირბადის ბოჭკოვანი გამაგრებული კომპოზიტური ლამინატის ფურცლის ფენოვანი გაფართოების ქცევის შესწავლა

გონგ იუ^1*, ვანგ იანა²პენგ ლეი³, ჟაო ლიბინი⁴ჟანგ ჯიანიუ¹

¹ჩონკინგის უნივერსიტეტი, ჩონკინგ, 400044, ჩინეთი
²ჩინეთის საავიაციო კვლევითი ინსტიტუტი, პეკინის აერონავტიკის მასალების კვლევითი ინსტიტუტი, პეკინი, 100095, ჩინეთი
³ჩინეთის კომერციული თვითმფრინავები პეკინის სამოქალაქო თვითმფრინავების ტექნოლოგიების კვლევითი ცენტრი, პეკინი, 102211, ჩინეთი
⁴პეკინის აერონავტიკისა და ასტრონავტიკის უნივერსიტეტი, პეკინი, 100191, ჩინეთი

აბსტრაქტულილამინირებული სტრუქტურა კომპოზიტებისთვის ერთ-ერთი ყველაზე ხშირად გამოყენებული კომპოზიტური კონფიგურაციაა, თუმცა სუსტი ფენებს შორისი თვისებების გამო მისი რღვევის მთავარი რეჟიმი დელამინირებაა. საინჟინრო პრაქტიკაში ფართოდ გამოყენებული მრავალშრიანი ლამინატის სტრატიფიკაციისა და გაფართოების ქცევის კვლევა ყოველთვის აქტუალური თემა იყო მეცნიერებისთვის. ამ ნაშრომში წარმოდგენილია ნახშირბადის ბოჭკოვანი გამაგრებული კომპოზიტის დელამინირების კვლევის შედეგები ჩონგკინგის უნივერსიტეტსა და პეკინის აერონავტიკისა და ასტრონავტიკის უნივერსიტეტის დაღლილობის მოტეხილობის ლაბორატორიაში ექსპერიმენტული კვლევისა და რიცხვითი სიმულაციის ორი ასპექტიდან. და ბოლოს, განხილულია დარგის განვითარების მიმართულება.

საკვანძო სიტყვები:ნახშირბადის ბოჭკოთი გამაგრებული კომპოზიტი, ლამინატი, დელამინირება, დაღლილობის სტრატიფიკაცია

შესავალი

კომპოზიტურ მასალებს აქვთ შესანიშნავი თვისებები, როგორიცაა მაღალი სპეციფიკური სიმტკიცე და მაღალი სპეციფიკური სიხისტე და ფართოდ გამოიყენება აერონავტიკაში, ენერგეტიკულ ტექნოლოგიებში, სამოქალაქო ტრანსპორტსა და მშენებლობაში. კომპოზიტური მასალების დამუშავებისა და გამოყენების დროს, ბოჭკოები და მატრიცა განიცდიან სხვადასხვა ხარისხის დაზიანებას დატვირთვის ქვეშ. კომპოზიტური ლამინირების საერთო უკმარისობის რეჟიმებია შრეებს შორის დაზიანება და ფენებში დაზიანება. სისქის მიმართულებით გამაგრების ნაკლებობის გამო, ლამინატის გვერდითი მექანიკური თვისებები ცუდია და დელამინაციის დაზიანების მაღალი ალბათობაა გარე დარტყმითი დატვირთვების ქვეშ. სტრატიფიცირებული დაზიანების წარმოქმნა და გაფართოება გამოიწვევს სტრუქტურული სიმტკიცისა და სიმტკიცის შემცირებას და კატასტროფულ ავარიებსაც კი.^[1-3]ამიტომ, დელამინაციის პრობლემა სულ უფრო მეტად ეხება კომპოზიტური მასალების სტრუქტურულ დიზაინსა და სიმტკიცის ანალიზს და აუცილებელია კომპოზიტური მასალების ფენოვანი გაფართოების ქცევის შესწავლა.^[4].

ლამინატის ფენოვანი გაფართოების ქცევის კვლევა
1. ექსპერიმენტული კვლევა

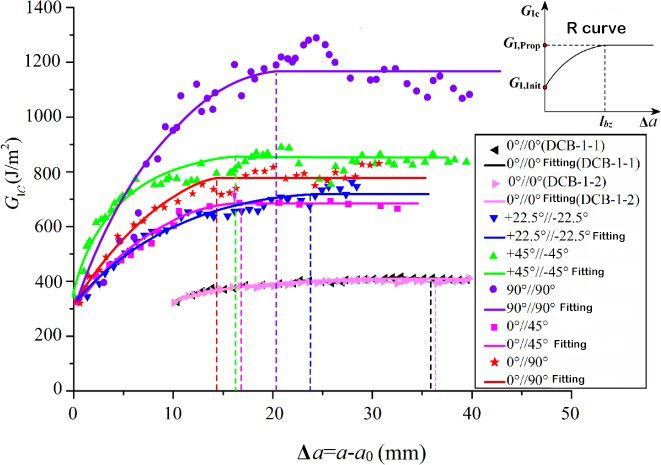
ფენებს შორის ფენოვანი მოტეხილობის სიმტკიცე კომპოზიტურ ფენებს შორის მექანიკური თვისებების დამახასიათებელი პარამეტრია. I, II ტიპის და I/II ჰიბრიდული ცალმხრივი მიმართულებითი ლამინატებისთვის ფენოვან მოტეხილობის სიმტკიცის დასადგენად დადგენილია შესაბამისი სატესტო სტანდარტები. შესაბამისი სატესტო აპარატურა ნაჩვენებია ნახაზ 1-ში. თუმცა, კომპოზიტური მასალების მრავალმხრივი მიმართულებითი ლამინატები ხშირად გამოიყენება რეალურ საინჟინრო სტრუქტურებში. ამიტომ, მრავალმხრივი მიმართულებითი ლამინატების სტრატიფიკაციისა და გაფართოების ქცევის ექსპერიმენტულ კვლევას უფრო მნიშვნელოვანი თეორიული მნიშვნელობა და საინჟინრო ღირებულება აქვს. მრავალმხრივი ლამინატის ფენის ინიცირება და გაფართოება ხდება თვითნებური შრეების კუთხის მქონე ინტერფეისებს შორის და ფენოვანი გაფართოების ქცევა მნიშვნელოვნად განსხვავდება ცალმხრივი მიმართულებითი ლამინატებისგან და გაფართოების მექანიზმი უფრო რთულია. მკვლევარებს შედარებით ცოტა ექსპერიმენტული კვლევა აქვთ მრავალმხრივ ლამინატებზე და ფენოვან მოტეხილობის სიმტკიცის განსაზღვრას ჯერ არ დაუდგენია საერთაშორისო სტანდარტი. კვლევითმა ჯგუფმა გამოიყენა T700 და T800 ნახშირბადის ბოჭკო სხვადასხვა კომპოზიტური ლამინატების შესაქმნელად სხვადასხვა ინტერფეისის განლაგების კუთხით და შეისწავლა ინტერფეისის განლაგების კუთხის და ბოჭკოების შეერთების გავლენა სტატიკურ და დაღლილობის დელამინაციის ქცევაზე. აღმოჩნდა, რომ ფენის უკანა კიდით წარმოქმნილი ბოჭკოვანი ხიდი დიდ გავლენას ახდენს ფენებს შორისი მოტეხილობის სიმტკიცეზე. სტრატიფიკაციის გაფართოებასთან ერთად, ფენებს შორისი მოტეხილობის სიმტკიცე თანდათან იზრდება უფრო დაბალი საწყისი მნიშვნელობიდან და როდესაც სტრატიფიკაცია გარკვეულ სიგრძეს მიაღწევს, ის აღწევს სტაბილურ მნიშვნელობას, ანუ R წინააღმდეგობის მრუდის ფენომენს. ფენებს შორისი ფენის საწყისი მოტეხილობის სიმტკიცე თითქმის ტოლია და დაახლოებით ტოლია ფისის მოტეხილობის სიმტკიცისა, რაც დამოკიდებულია თავად მატრიცის მოტეხილობის სიმტკიცეზე.^{[5, 6]}თუმცა, სხვადასხვა ინტერფეისების ფენებს შორის მოტეხილობის სიმტკიცის გაფართოების მნიშვნელობები მნიშვნელოვნად განსხვავდება. წარმოდგენილია ინტერფეისის ფენის კუთხის მნიშვნელოვანი დამოკიდებულება. ამ დამოკიდებულების საპასუხოდ, ჟაო და სხვ.^[5]სტრატიფიცირებული წინააღმდეგობის წყაროს ფიზიკური მექანიზმის საფუძველზე, ითვლება, რომ ფენებს შორისი მოტეხილობის სიმტკიცის სტაბილურობის მნიშვნელობა ორი ნაწილისგან შედგება, ერთი ნაწილი არის დაუკავშირებელი ფენის ინტერფეისის მოტეხილობის სამუშაო, ხოლო მეორე ნაწილი არის ფენის შიდა დაზიანება და ბოჭკო. მოტეხილობის სამუშაო, რომელიც გამოწვეულია ხიდით. ფენიანი ფრონტის დაძაბულობის ფრონტის ველის სასრული ელემენტების ანალიზის მეშვეობით დადგინდა, რომ მოტეხილობის მუშაობის მეორე ნაწილი დამოკიდებულია დელამინაციის ფრონტის დაზიანების ზონის სიღრმეზე (როგორც ნაჩვენებია ნახაზ 3-ში) და დაზიანების ზონის სიღრმე პროპორციულია ინტერფეისის განლაგების კუთხისა. წარმოდგენილია I-ტიპის მოტეხილობის სიმტკიცის სტაბილურობის მნიშვნელობის თეორიული მოდელი, რომელიც გამოხატულია ინტერფეისის ფენის კუთხის სინუსოიდური ფუნქციით.
გონგი და სხვ.^[7]ჩაატარა I/II ჰიბრიდული სტრატიფიკაციის ტესტი სხვადასხვა შერევის თანაფარდობით და აღმოაჩინა, რომ ლამინატში I/II ჰიბრიდულ სტრატიფიკაციას ასევე აქვს მნიშვნელოვანი R წინააღმდეგობის მრუდის მახასიათებლები. სხვადასხვა საცდელ ნაწილებს შორის მოტეხილობის სიმტკიცის ანალიზით დადგინდა, რომ საცდელი ნაწილის ფენებს შორის მოტეხილობის სიმტკიცის საწყისი და სტაბილური მნიშვნელობა მნიშვნელოვნად იზრდება შერევის თანაფარდობის ზრდასთან ერთად. გარდა ამისა, სხვადასხვა შერევის თანაფარდობით შუალედური ფენის საწყისი და სტაბილური მოტეხილობის სიმტკიცე შეიძლება აღიწეროს BK კრიტერიუმით.
დაღლილობის სტრატიფიკაციის თვალსაზრისით, ტესტის დროს ასევე დაფიქსირდა ბოჭკოების მნიშვნელოვანი შეერთება. ტესტის მონაცემების ანალიზით დადგინდა, რომ კომპოზიტური მასალის დაღლილობის დელამინაციის გაფართოებაზე გავლენას ახდენს „წინააღმდეგობის მრუდი“, რის გამოც ტრადიციული დაღლილობის სტრატიფიკაციის გაფართოების სიჩქარის მოდელი და ზღვრული მნიშვნელობა აღარ არის გამოსაყენებელი. თეორიული ანალიზის საფუძველზე, ჟანგმა და პენგმა...^[4,8,9]კომპოზიტური მასალების დაღლილობის დელამინაციის გაფართოებისთვის საჭირო ენერგიის გამოსახატავად შემოიღო დაღლილობის დელამინაციის გაფართოების წინააღმდეგობა და შემდგომ შემოგვთავაზა ნორმალიზებული დეფორმაციის ენერგია. გამოთავისუფლების სიჩქარე არის დაღლილობის სტრატიფიცირებული გაფართოების სიჩქარის მოდელი და საკონტროლო პარამეტრების ზღურბლოვანი მნიშვნელობა. მოდელისა და ნორმალიზებული ზღურბლოვანი პარამეტრის გამოყენებადობა დადასტურებულია ექსპერიმენტებით. გარდა ამისა, ჟაო და სხვ.^[3]ყოვლისმომცველად განიხილეს ბოჭკოვანი შეერთების, დაძაბულობის კოეფიციენტის და დატვირთვა-შერევის კოეფიციენტის გავლენა დაღლილობის სტრატიფიკაციასა და გაფართოების ქცევაზე და შექმნეს ნორმალიზებული დაღლილობის სტრატიფიცირებული გაფართოების სიჩქარის მოდელი, დაძაბულობის კოეფიციენტის გავლენის გათვალისწინებით. მოდელის სიზუსტე დადასტურდა დაღლილობის სტრატიფიკაციის ტესტებით სხვადასხვა დაძაბულობის კოეფიციენტებით და შერევის კოეფიციენტებით. ნორმალიზებული დაღლილობის სტრატიფიცირებული გაფართოების სიჩქარის მოდელში დაღლილობის სტრატიფიცირებული გაფართოების წინააღმდეგობის ფიზიკური რაოდენობისთვის, გონგმა და სხვებმა...^[1]გამოთვლის მეთოდის სისუსტის დაძლევა, რომელსაც ექსპერიმენტების საშუალებით მხოლოდ შეზღუდული დისკრეტული მონაცემების მიღება შეუძლია და დაღლილობის დადგენა ენერგიის თვალსაზრისით. სტრატიფიცირებული გაფართოებული წინაღობის გაანგარიშების ანალიტიკური მოდელი. მოდელს შეუძლია დაღლილობის სტრატიფიკაციისა და გაფართოების წინაღობის რაოდენობრივი განსაზღვრის განხორციელება და თეორიული მხარდაჭერის უზრუნველყოფა შემოთავაზებული ნორმალიზებული დაღლილობის სტრატიფიცირებული გაფართოების სიჩქარის მოდელის გამოყენებისთვის.

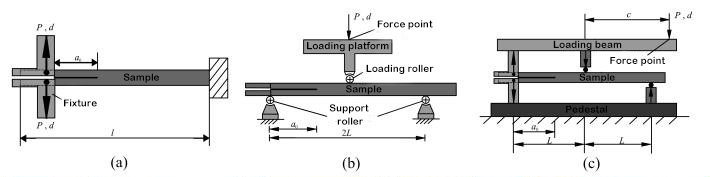სურათი 1. სტრატიფიცირებული ტესტის მოწყობილობის დიაგრამა

სურათი 2. შრეთაშორისი მსხვრევადი სიმტკიცის R წინააღმდეგობის მრუდი^[5]


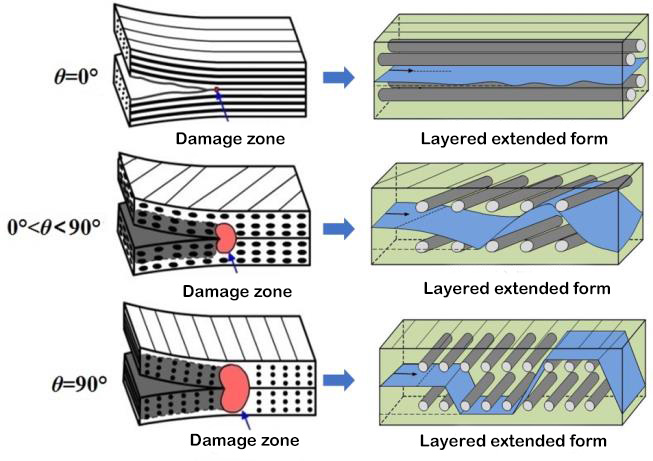
სურათი 3. წამყვანი კიდის დაზიანების ფენიანი ზონა და სტრატიფიცირებული გაფართოებული მორფოლოგია^[5]

2. რიცხვითი სიმულაციის შესწავლა

ფენოვანი გაფართოების რიცხვითი სიმულაცია კომპოზიტური სტრუქტურის დიზაინის სფეროში მნიშვნელოვანი კვლევის შინაარსია. კომპოზიტური ცალმხრივი მიმართულებითი ლამინირების დელამინაციის უკმარისობის პროგნოზირებისას, არსებული სტრატიფიკაციის გაფართოების კრიტერიუმები, როგორც წესი, ძირითად მახასიათებლად იყენებს მუდმივ ფენებს შორის მსხვრევად სიმტკიცეს.^[10], ბზარის წვერის ენერგიის გამოთავისუფლების სიჩქარისა და ფენებს შორისი მოტეხილობის სიმტკიცის შედარებით. ზომა იმის დასადგენად, ფართოვდება თუ არა ფენა. მრავალმიმართულებიანი ლამინატის რღვევის მექანიზმი რთულია.^[11,12], რომელიც ხასიათდება მნიშვნელოვანი R წინააღმდეგობის მრუდებით^[5,13]არსებული ფენოვანი გაფართოების კრიტერიუმები არ ითვალისწინებს ამ მახასიათებელს და არ გამოიყენება ბოჭკოვანი ხიდის შემცველი მრავალმხრივი ლამინირების დელამინაციის ქცევის სიმულაციისთვის. გონგი და სხვ.^{[10, 13]}გააუმჯობესა არსებული სტრატიფიცირებული გაფართოების კრიტერიუმები და შესთავაზა კრიტერიუმებში R წინააღმდეგობის მრუდის შეტანა და ამის საფუძველზე შეიქმნა სტრატიფიცირებული გაფართოების კრიტერიუმი ბოჭკოვანი შეერთების ეფექტების გათვალისწინებით. ორწრფივი შემადგენელი შეკრული ერთეულის განმარტებისა და გამოყენების პარამეტრები სისტემატურად იქნა შესწავლილი რიცხვითი მეთოდებით, მათ შორის საწყისი ინტერფეისის სიმტკიცე, ინტერფეისის სიმტკიცე, სიბლანტის კოეფიციენტი და ელემენტების მინიმალური რაოდენობა შეკრული ძალის ზონაში. დადგინდა შესაბამისი შეკრული ერთეულის პარამეტრის მოდელი. დაბოლოს, გაუმჯობესებული ფენოვანი გაფართოების კრიტერიუმისა და შეკრული ერთეულის პარამეტრის მოდელის ეფექტურობა და გამოყენებადობა დადასტურებულია სტატიკური სტრატიფიკაციის ტესტით. თუმცა, გაუმჯობესებული კრიტერიუმების გამოყენება შესაძლებელია მხოლოდ ერთგანზომილებიანი ფენოვანი სიმულაციებისთვის პოზიციური დამოკიდებულების გამო და არა ორ ან სამგანზომილებიანი იერარქიული გაფართოებებისთვის. ამ პრობლემის გადასაჭრელად, ავტორმა ასევე შემოგვთავაზა ახალი სამწრფივი შეკრული ძალის შემადგენელი, ბოჭკოვანი შეერთების გათვალისწინებით.^[14]კონსტიტუციური ურთიერთობა მიკროსკოპული პერსპექტივიდან შეესაბამება ფენოვანი გაფართოების რთულ პროცესს და აქვს მარტივი პარამეტრებისა და მკაფიო ფიზიკური მნიშვნელობის უპირატესობები.
გარდა ამისა, მრავალმხრივი ლამინატის სტრატიფიკაციის პროცესში გავრცელებული სტრატიფიცირებული მიგრაციის ფენომენის ზუსტად სიმულირებისთვის^[11,12], ჟაო და სხვ.^[11,12]შემოთავაზებულია გაფართოებული სასრული ელემენტის საფუძველზე შექმნილი ბზარის ტრაექტორიის მართვის მოდელი, რომელიც ახდენს სპეციალური დიზაინის სიმულირებას. იერარქიული მიგრაცია კომპოზიტური სტრატიფიკაციის ტესტში. ამავდროულად, შემოთავაზებულია ფენოვანი გაფართოების მოდელი ზიგზაგისებური ფენოვანი გაფართოების ქცევისთვის 90°/90° ფენოვანი ინტერფეისის გასწვრივ, რომელიც ზუსტად ახდენს 90°/90° ინტერფეისის ფენოვანი გაფართოების ქცევის სიმულირებას.

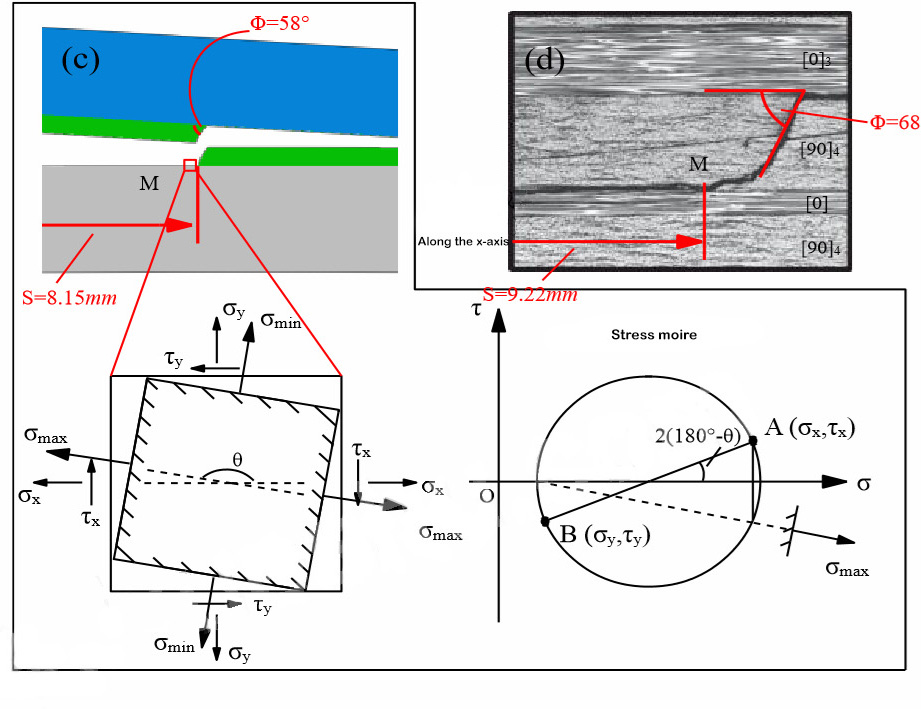სურათი 4. ფენიანი მიგრაციის რიცხვითი სიმულაცია და ექსპერიმენტული შედეგები^[15]

დასკვნა

ეს ნაშრომი ფოკუსირებულია ამ ჯგუფის კვლევის შედეგებზე კომპოზიტური ლამინატის დელამინირების სფეროში. ექსპერიმენტული ასპექტები ძირითადად მოიცავს ინტერფეისის განლაგების კუთხის და ბოჭკოვანი ხიდის გავლენას სტატიკურ და დაღლილობის დელამინაციის გაფართოების ქცევაზე. ექსპერიმენტული კვლევების დიდი რაოდენობით შედეგად დადგინდა, რომ კომპოზიტური მასალების მრავალმიმართულებიანი ლამინატის რღვევის მექანიზმი რთულია. ბოჭკოვანი ხიდი მრავალმიმართულებიანი ლამინატებისთვის გავრცელებული გამკვრივების მექანიზმია, რაც წარმოადგენს ფენებს შორისი მოტეხილობის სიმტკიცის R-წინააღმდეგობის მრუდის მთავარ მიზეზს. ამჟამად, II სტრატიფიკაციის ქვეშ R წინააღმდეგობის მრუდის შესწავლა შედარებით არასრულია და საჭიროებს შემდგომ კვლევას. რღვევის მექანიზმიდან დაწყებული, შემოთავაზებულია დაღლილობის სტრატიფიკაციის მოდელი, რომელიც მოიცავს სხვადასხვა გავლენის ფაქტორებს, რაც დაღლილობის სტრატიფიკაციის კვლევის ერთ-ერთი მიმართულებაა. რიცხვითი სიმულაციის თვალსაზრისით, კვლევითმა ჯგუფმა შემოგვთავაზა გაუმჯობესებული იერარქიული გაფართოების კრიტერიუმი და შეკრული კონსტიტუციური მოდელი, რათა გათვალისწინებულ იქნას ბოჭკოვანი ხიდის გავლენა სტრატიფიცირებულ გაფართოების ქცევაზე. გარდა ამისა, გაფართოებული სასრული ელემენტი გამოიყენება იერარქიული მიგრაციის ფენომენის უკეთ სიმულირებისთვის. ეს მეთოდი გამორიცხავს წვრილი უჯრედების დაყოფის საჭიროებას, რაც აღმოფხვრის ბადის ხელახლა დაყოფასთან დაკავშირებულ პრობლემებს. მას უნიკალური უპირატესობები აქვს თვითნებური ფორმების სტრატიფიკაციის სიმულაციაში და მომავალში ამ მეთოდის საინჟინრო გამოყენების მეტი კვლევაა საჭირო.^[16].

ცნობები

[1] ი. გონგი, ლ. ჟაო, ჯ. ჟანგი, ნ. ჰუ. კომპოზიტურ ლამინატში დაღლილობის დელამინაციისადმი წინააღმდეგობის განსაზღვრის ახალი მოდელი ენერგიის თვალსაზრისით. Compos Sci Technol 2018; 167: 489-96.
[2] ლ. ჟაო, ი. ვანგი, ჯ. ჟანგი, ი. გონგი, ნ. ჰუ, ნ. ლი. XFEM-ზე დაფუძნებული მოდელი ლამინირებულ კომპოზიტებში ზიგზაგისებური დელამინაციის ზრდის სიმულირებისთვის I რეჟიმის დატვირთვის ქვეშ. Compos Struct 2017; 160: 1155-62.
[3] ლ. ჟაო, ი. გონგი, ჯ. ჟანგი, ი. ვანგი, ზ. ლუ, ლ. პენგი, ნ. ჰუ. დაღლილობის შედეგად დელამინაციის ზრდის ქცევის ახალი ინტერპრეტაცია CFRP მრავალმხრივ ლამინატში. Compos Sci Technol 2016; 133: 79-88.
[4] ლ. პენგი, ჯ. ჟანგი, ლ. ჟაო, რ. ბაო, ჰ. იანგი, ბ. ფეი. მრავალმხრივი კომპოზიტური ლამინირების I რეჟიმის დელამინაციის ზრდა დაღლილობის დატვირთვის ქვეშ. J Compos Mater 2011; 45: 1077-90.
[5] ლ. ჟაო, ი. ვანგი, ჯ. ჟანგი, ი. გონგი, ზ. ლუ, ნ. ჰუ, ჯ. სიუ. მრავალმხრივი CFRP ლამინატების პლატოსებრი მოტეხილობის სიმტკიცის ინტერფეის-დამოკიდებული მოდელი I რეჟიმის დატვირთვის ქვეშ. კომპოზიტები, ნაწილი B: ინჟინერია 2017; 131: 196-208.
[6] ლ. ჟაო, ი. გონგი, ჯ. ჟანგი, ი. ჩენი, ბ. ფეი. მრავალმიმართულებიან ლამინატში დელამინაციის ზრდის სიმულაცია I რეჟიმის და შერეული რეჟიმის I/II დატვირთვების დროს შეკრული ელემენტების გამოყენებით. Compos Struct 2014; 116: 509-22.
[7] ი. გონგი, ბ. ჟანგი, ლ. ჟაო, ჯ. ჟანგი, ნ. ჰუ, ს. ჟანგი. შერეული რეჟიმის I/II დელამინაციის R-მრუდის ქცევა ნახშირბადის/ეპოქსიდის ლამინატში ცალმხრივი და მრავალმხრივი ინტერფეისებით. Compos Struct 2019. (მიმდინარეობს მიმოხილვა).
[8] ლ. პენგი, ჯ. სიუ, ჯ. ჟანგი, ლ. ჟაო. მრავალმხრივი კომპოზიტური ლამინირების შერეული რეჟიმის დელამინირების ზრდა დაღლილობის დატვირთვის ქვეშ. Eng Fract Mech 2012; 96: 676-86.
[9] ჯ. ჟანგი, ლ. პენგი, ლ. ჟაო, ბ. ფეი. შერეული რეჟიმის დატვირთვის ქვეშ კომპოზიტური ლამინირების დაღლილობის დელამინაციის ზრდის ტემპები და ზღურბლები. Int J Fatigue 2012; 40: 7-15.
[10] ი. გონგი, ლ. ჟაო, ჯ. ჟანგი, ი. ვანგი, ნ. ჰუ. დელამინაციის გავრცელების კრიტერიუმი, მათ შორის ბოჭკოვანი ხიდის ეფექტი შერეული რეჟიმის I/II დელამინაციისთვის CFRP მრავალმიმართულებიან ლამინატში. Compos Sci Technol 2017; 151: 302-9.
[11] ი. გონგი, ბ. ჟანგი, ს.რ. ჰალეტი. მრავალმიმართულებიანი კომპოზიტური ლამინატების დელამინაციის მიგრაცია I რეჟიმის კვაზისტატიკური და დაღლილობის დატვირთვის ქვეშ. Compos Struct 2018; 189: 160-76.
[12] ი. გონგი, ბ. ჟანგი, ს. მუხოპადჰიაი, ს.რ. ჰალეტი. მრავალმიმართულებიანი ლამინატების დელამინაციის მიგრაციის ექსპერიმენტული კვლევა II რეჟიმის სტატიკური და დაღლილობის დატვირთვის ქვეშ, I რეჟიმთან შედარებით. Compos Struct 2018; 201: 683-98.
[13] ი გონგი, ლ ჟაო, ჯ ჟანგი, ნ ჰუ. კომპოზიტურ მრავალმიმართულებიან ლამინატში ფართომასშტაბიანი ბოჭკოვანი ხიდის ეფექტით დელამინაციის გავრცელების გაუმჯობესებული ხარისხის კანონის კრიტერიუმი. Compos Struct 2018; 184: 961-8.
[14] ი გონგი, ი ჰოუ, ლ ჟაო, ვ ლი, გ იანგი, ჯ ჟანგი, ნ ჰუ. ბოჭკოვანი ხიდის ეფექტით DCB ლამინატების დელამინაციის ზრდის ახალი სამხაზოვანი შეკავშირებული ზონის მოდელი. Compos Struct 2019. (წარსადგენია)
[15] ლ. ჟაო, ჯ. ჟი, ჯ. ჟანგი, ზ. ლიუ, ნ. ჰუ. კომპოზიტურ ლამინატში დელამინაციის XFEM სიმულაცია. კომპოზიტები, ნაწილი A: გამოყენებითი მეცნიერება და წარმოება 2016; 80: 61-71.
[16] ჟაო ლიბინი, გონგ იუ, ჟანგ ჯიანიუ. ბოჭკოვანი გამაგრებული კომპოზიტური ლამინირების სტრატიფიცირებული გაფართოების ქცევის კვლევის პროგრესი. აერონავტიკის მეცნიერებათა ჟურნალი 2019: 1-28.

წყარო:გონგ იუ, ვანგ იანა, პენგ ლეი, ჟაო ლიბინი, ჟანგ ჯიანიუ. ნახშირბადის ბოჭკოთი გამაგრებული კომპოზიტური ლამინირების სტრატიფიცირებული გაფართოების ქცევის კვლევა [C]. მექანიკა და ინჟინერია - რიცხვითი გამოთვლები და მონაცემთა ანალიზი, 2019 წლის აკადემიური კონფერენცია. ჩინეთის მექანიკის საზოგადოება, პეკინის მექანიკის საზოგადოება, 2019. გავლით იქსუესუ