GÉPÉSZET ÉS MŰSZAKI TUDOMÁNYOK - Numerikus számítás és adatelemzés
Mechanika és Mérnöki Tudományok — Numerikus Számítások és Adatelemzés 2019 Akadémiai Konferencia, 2019. április 19-21., Peking
2019. április 19-21., Peking, Kína
Tanulmány a fejlett szénszálerősítésű kompozit laminált lemez réteges tágulási viselkedéséről
Gong Yu1*, Vang Jana2, Peng Lei3, Zhao Libin4, Zhang Jianyu1
1Csungkingi Egyetem, Csungking, 400044, Kína
2Kínai Repülési Kutatóintézet, Pekingi Repülési Anyagkutató Intézet, Peking, 100095, Kína
3Kínai Kereskedelmi Repülőgépek Pekingi Polgári Repülőgép Technológiai Kutatóközpont, Peking, 102211, Kína
4Pekingi Repüléstudományi és Űrhajózási Egyetem, Peking, 100191, Kína
AbsztraktA laminált szerkezet az egyik leggyakrabban használt kompozit konfiguráció a kompozitok esetében, de a gyenge rétegek közötti tulajdonságok miatt a delamináció válik a fő meghibásodási móddá. A mérnöki gyakorlatban általánosan alkalmazott többrétegű laminátumok rétegződésével és tágulási viselkedésével kapcsolatos kutatások mindig is forró téma voltak a tudósok számára. Ebben a cikkben a Csungkingi Egyetem és a Pekingi Repüléstudományi és Űrhajózási Egyetem Fáradásos Törés Laboratóriumában végzett szénszálas erősítésű kompozit delaminációval kapcsolatos kutatási eredményeket mutatjuk be a kísérleti kutatás és a numerikus szimuláció két aspektusából. Végül a terület fejlődési irányát is felvázoljuk.
Kulcsszavak:szénszállal erősített kompozit, laminátum, delamináció, kifáradásos rétegződés
bevezetés
A kompozit anyagok kiváló tulajdonságokkal rendelkeznek, mint például a nagy fajlagos szilárdság és a nagy fajlagos merevség, és széles körben használják őket a repülőgépiparban, az energetikai technológiában, valamint a polgári közlekedésben és építőiparban. A kompozit anyagok feldolgozása és felhasználása során a szálak és a mátrix terhelés alatt különböző mértékű károsodást szenvednek. A kompozit laminátumok gyakori meghibásodási módjai közé tartozik a rétegek közötti károsodás és a rétegeken belüli károsodás. A vastagságirányban lévő erősítés hiánya miatt a laminátum oldalirányú mechanikai tulajdonságai gyengék, és külső ütőterhelések hatására nagy valószínűséggel delaminációs károsodás lép fel. A réteges károsodás előfordulása és kiterjedése a szerkezeti merevség és szilárdság csökkenéséhez vezet, sőt katasztrofális baleseteket is okozhat.[1-3]Ezért a delaminációs probléma egyre inkább aggasztja a kompozit anyagok szerkezeti tervezését és szilárdsági elemzését, és szükséges a kompozit anyagok réteges tágulási viselkedésének tanulmányozása.[4].
A laminátum réteges tágulási viselkedésének kutatása
1. Kísérleti tanulmány
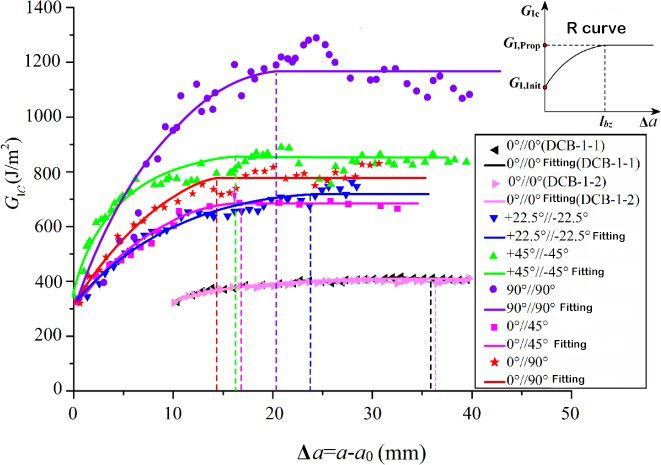
A rétegek közötti törési szívósság a kompozit rétegek közötti mechanikai tulajdonságok jellemző paramétere. Megfelelő vizsgálati szabványokat dolgoztak ki az I., II. típusú és I/II. típusú hibrid egyirányú laminátumok rétegek közötti törési szívósságának meghatározására. A megfelelő vizsgálati berendezés az 1. ábrán látható. A kompozit anyagok többirányú laminátumait azonban gyakran használják a tényleges mérnöki szerkezetekben. Ezért a többirányú laminátumok rétegződési és tágulási viselkedésének kísérleti vizsgálata fontosabb elméleti jelentőséggel és mérnöki értékkel bír. A többrétegű laminátum réteg iniciációja és tágulása tetszőleges rétegződési szögű határfelületek között történik, és a réteges tágulási viselkedés jelentősen eltér az egyirányú laminátumokétól, és a tágulási mechanizmus bonyolultabb. A kutatók viszonylag kevés kísérleti vizsgálattal rendelkeznek a többirányú laminátumokról, és a rétegek közötti törési szívósság meghatározása még nem hozott létre nemzetközi szabványt. A kutatócsoport T700 és T800 szénszálakat használt különféle kompozit laminátumok tervezéséhez különböző határfelületi rétegződési szögekkel, és vizsgálta a határfelületi rétegződési szög és a szálak áthidalásának hatását a statikus és fáradásos delaminációs viselkedésre. Megállapították, hogy a réteg kilépő éle által létrehozott szálhidak nagy hatással vannak a rétegek közötti törési szívósságra. Ahogy a rétegződés kiterjed, a rétegek közötti törési szívósság fokozatosan növekszik egy alacsonyabb kezdeti értékről, és amikor a rétegződés eléri az adott hosszúságot, stabil értéket ér el, azaz az R ellenállási görbe jelenségét. A közbenső réteg kezdeti törési szívóssága majdnem megegyezik és megközelítőleg megegyezik a gyanta törési szívósságával, amely maga a mátrix törési szívósságától függ.[5, 6]A különböző határfelületek rétegek közötti törési szívósság kiterjedésének értékei azonban nagymértékben eltérnek. Jelentős határfelületi réteg szögfüggést mutatnak be. Erre a függőségre válaszul Zhao és munkatársai...[5]A rétegzett ellenállásforrás fizikai mechanizmusa alapján úgy véljük, hogy a rétegek közötti törési szívósság stabilitási értéke két részből áll: az egyik rész a nem kapcsolódó réteghatár törési munkája, a másik rész pedig a rétegen belüli károsodás és a szál. Az áthidalás okozta törés munkája. A réteges front feszültségfront mezőjének végeselemes elemzésén keresztül megállapítottuk, hogy a törési munka második része a delaminációs front károsodási zónájának mélységétől függ (ahogy a 3. ábra mutatja), és a károsodási zóna mélysége arányos a határfelület rétegződési szögével. Bemutatunk egy elméleti modellt az I-típusú törési szívósság stabilitási értékéről, amelyet a határfelületi réteg szögének szinuszos függvénye fejez ki.
Gong és mtsai.[7]elvégezte az I/II hibrid rétegződési vizsgálatot különböző keverési arányok mellett, és megállapította, hogy a laminátum I/II hibrid rétegződése jelentős R ellenállási görbe jellemzőkkel is rendelkezik. A különböző tesztdarabok törési szívósságának elemzésével megállapították, hogy a tesztdarab rétegek közötti törési szívósságának kezdeti értéke és stabil értéke jelentősen növekszik a keverési arány növekedésével. Ezenkívül a közbenső réteg kezdeti és stabil törési szívóssága különböző keverési arányok mellett a BK kritériummal leírható.
A fáradásos rétegződés tekintetében a vizsgálat során jelentős száláthidalás is megfigyelhető volt. A vizsgálati adatok elemzésével megállapították, hogy a kompozit anyag fáradásos delaminációjának tágulását befolyásolja az „ellenállási görbe”, így a hagyományos fáradásos rétegződés tágulási sebességmodellje és a küszöbérték már nem alkalmazható. Az elméleti elemzés alapján Zhang és Peng[4,8,9]bevezette a fáradásos delamináció miatti tágulási ellenállást a kompozit anyagok fáradásos delaminációjához szükséges energia kifejezésére, és javasolta továbbá a normalizált alakváltozási energiát. A kibocsátási sebesség a fáradásos rétegzett tágulási sebesség modellje és a szabályozási paraméterek küszöbértéke. A modell és a normalizált küszöbparaméter alkalmazhatóságát kísérletekkel igazolták. Továbbá Zhao és munkatársai...[3]átfogóan vizsgálta a száláthidalás, a feszültségviszony és a terhelés-keverési arány hatását a fáradási rétegződésre és a tágulási viselkedésre, és létrehozott egy normalizált fáradási rétegzett tágulási sebességmodellt, figyelembe véve a feszültségviszony hatását. A modell pontosságát különböző feszültségviszonyokkal és keverési arányokkal végzett fáradási rétegződési vizsgálatokkal igazolták. A normalizált fáradási rétegzett tágulási sebességmodellben a fáradási rétegzett tágulási ellenállás fizikai mennyiségére Gong és munkatársai...[1]A számítási módszer azon gyengeségének leküzdésére, amely csak korlátozott diszkrét adatpontokat képes kísérletekkel nyerni, és az energia szempontjából megállapítani a fáradást. Egy analitikus modell a rétegzett kiterjesztett ellenállás kiszámítására. A modell képes megvalósítani a fáradási rétegződés és a tágulási ellenállás kvantitatív meghatározását, és elméleti támogatást nyújt a javasolt normalizált fáradási rétegzett tágulási sebességmodell alkalmazásához.
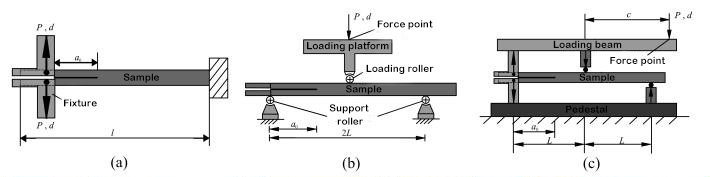1. ábra rétegzett teszteszköz diagramja
2. ábra Rétegek közötti törési szívósság R ellenállási görbéje[5]
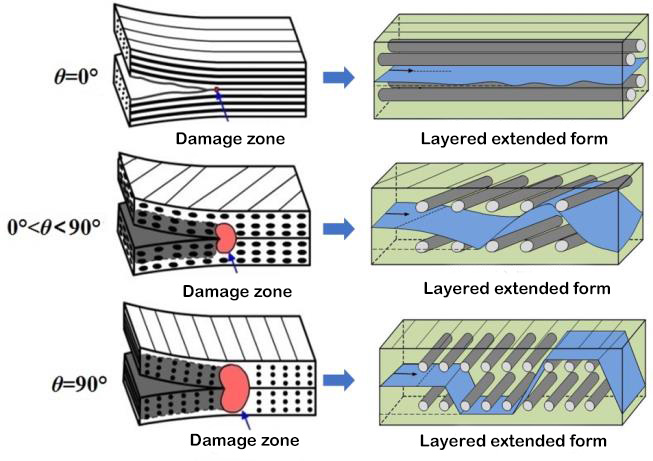
3. ábra Réteges belépőél károsodási zóna és rétegzett kiterjesztett morfológia[5]
2. Numerikus szimulációs tanulmány
A réteges tágulás numerikus szimulációja fontos kutatási terület a kompozit szerkezettervezés területén. Az egyirányú kompozit laminátumok delaminációs törésének előrejelzésekor a meglévő réteges tágulási kritériumok általában az állandó rétegek közötti törési szívósságot használják alapvető teljesítményparaméterként.[10], a repedéscsúcs energiafelszabadulási sebességének és a rétegek közötti törési szívósság összehasonlításával. Méret annak meghatározására, hogy a rétegződés tágul-e. A többirányú laminátumok törési mechanizmusa összetett[11,12], amelyet jelentős R ellenállásgörbék jellemeznek[5,13]A meglévő réteges expanziós kritériumok nem veszik figyelembe ezt a tulajdonságot, és nem vonatkoznak a szálakat tartalmazó áthidalt, többirányú laminátumok delaminációs viselkedésének szimulációjára. Gong et al.[10, 13]továbbfejlesztette a meglévő rétegzett expanziós kritériumokat, és javasolta az R ellenállási görbe bevezetését a kritériumokba, és ennek alapján létrehozott egy rétegzett expanziós kritériumot, figyelembe véve a szálak áthidalásának hatásait. A bilineáris konstitutív kohéziós egység definícióját és felhasználási paramétereit szisztematikusan vizsgálták numerikus módszerekkel, beleértve a kezdeti határfelületi merevséget, a határfelületi szilárdságot, a viszkozitási együtthatót és a kohéziós erő zónájában lévő elemek minimális számát. Megállapították a megfelelő kohéziós egység paramétermodelljét. Végül a továbbfejlesztett rétegzett expanziós kritérium és a kohéziós egység paramétermodell hatékonyságát és alkalmazhatóságát statikus rétegződési vizsgálattal igazolták. A továbbfejlesztett kritériumok azonban a pozicionális függőségek miatt csak egydimenziós rétegzett szimulációkhoz használhatók, két- vagy háromdimenziós hierarchikus kiterjesztésekhez nem. A probléma megoldása érdekében a szerző egy új, trilineáris kohéziós erő konstitutív kritériumát javasolta, figyelembe véve a szálak áthidalását.[14]A konstitutív kapcsolat mikroszkopikus szempontból illik a réteges tágulás összetett folyamatához, és az egyszerű paraméterek, valamint a világos fizikai jelentés előnyeivel rendelkezik.
Ezenkívül a többirányú laminátumok rétegződési folyamatában gyakori rétegzett migrációs jelenség pontos szimulálása érdekében[11,12], Zhao és mtsai.[11,12]egy kiterjesztett végeselemes módszeren alapuló repedéspálya-vezetési modellt javasolt, amely egy speciális tervet szimulál. Hierarchikus migráció egy összetett rétegződési vizsgálatban. Ugyanakkor egy réteges tágulási modellt javasol a cikkcakk réteges tágulási viselkedésre a 90°/90°-os réteges határfelület mentén, amely pontosan szimulálja a 90°/90°-os határfelület réteges tágulási viselkedését.
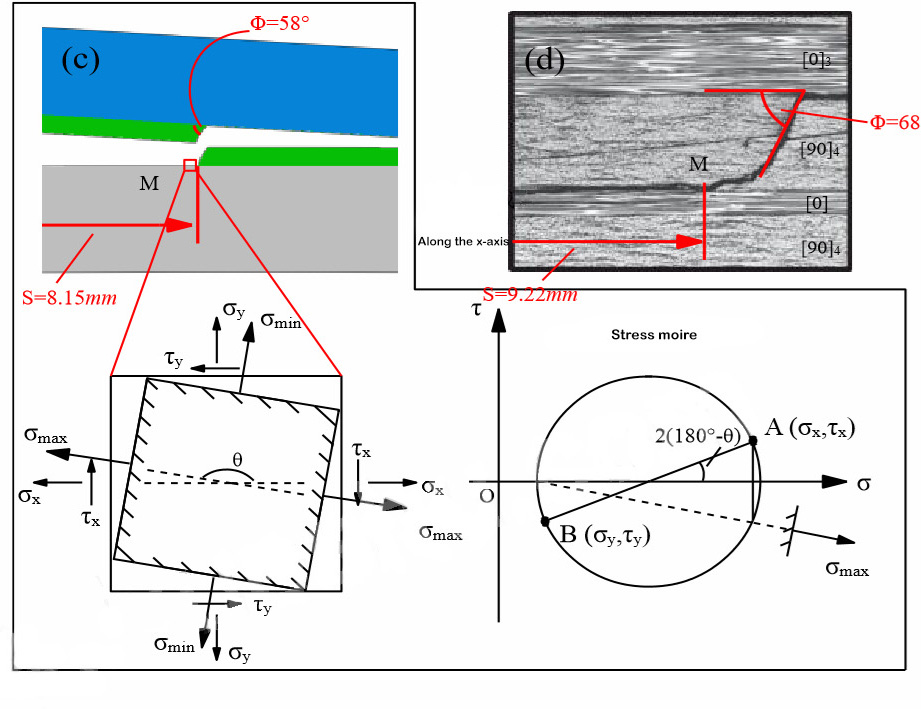4. ábra A réteges migráció numerikus szimulációja és a kísérleti eredmények[15]
Következtetés
Ez a tanulmány a kutatócsoport kutatási eredményeire összpontosít a kompozit laminátumok delaminációjának területén. A kísérleti szempontok főként a határfelületi rétegződési szög és a szálak áthidalódásának a statikus és fáradásos delamináció tágulási viselkedésére gyakorolt hatását foglalják magukban. Számos kísérleti vizsgálat alapján megállapították, hogy a kompozit anyagok többirányú laminátum-törési mechanizmusa bonyolult. A szálak áthidalódása a többirányú laminátumok gyakori edzési mechanizmusa, ami a rétegek közötti törési szívósság R-ellenállási görbéjének fő oka. Jelenleg az R ellenállási görbe vizsgálata a II rétegződés alatt viszonylag hiányos, és további kutatásokra van szükség. A törési mechanizmusból kiindulva javaslatot tesznek egy különböző befolyásoló tényezőket magában foglaló fáradási rétegződési modellre, amely a fáradási rétegződés kutatásának egyik iránya. A numerikus szimuláció tekintetében a kutatócsoport egy továbbfejlesztett hierarchikus tágulási kritériumot és egy koherens konstitutív modellt javasolt a szálak áthidalódásának a rétegzett tágulási viselkedésre gyakorolt hatásának figyelembevételére. Ezenkívül a kiterjesztett végeselemes módszert alkalmazzák a hierarchikus migrációs jelenség jobb szimulálására. Ez a módszer kiküszöböli a finom cellafelosztás szükségességét, kiküszöbölve a háló újrafelosztásával kapcsolatos problémákat. Egyedülálló előnyökkel rendelkezik a tetszőleges alakzatok rétegződésének szimulációjában, és a jövőben további mérnöki alkalmazáskutatásokra van szükség e módszerrel kapcsolatban.[16].
Referenciák
[1] Y Gong, L Zhao, J Zhang, N Hu. Új modell a kompozit laminátumok fáradásos delaminációval szembeni ellenállásának meghatározására energia szempontjából. Compos Sci Technol 2018; 167: 489-96.
[2] L Zhao, Y Wang, J Zhang, Y Gong, N Hu, N Li. XFEM-alapú modell a cikkcakk delamináció növekedésének szimulálására laminált kompozitokban I. módú terhelés alatt. Compos Struct 2017; 160: 1155-62.
[3] L Zhao, Y Gong, J Zhang, Y Wang, Z Lu, L Peng, N Hu. A fáradásos delamináció növekedési viselkedésének új értelmezése CFRP többirányú laminátumokban. Compos Sci Technol 2016; 133: 79-88.
[4] L Peng, J Zhang, L Zhao, R Bao, H Yang, B Fei. Többirányú kompozit laminátumok I. módú delaminációjának növekedése fárasztó terhelés alatt. J Compos Mater 2011; 45: 1077-90.
[5] L Zhao, Y Wang, J Zhang, Y Gong, Z Lu, N Hu, J Xu. Felületfüggő modell a plató törési szívósságára többirányú CFRP laminátumokban I. módú terhelés alatt. Composites Part B: Engineering 2017; 131: 196-208.
[6] L Zhao, Y Gong, J Zhang, Y Chen, B Fei. Többirányú laminátumok delaminációnövekedésének szimulációja I. módú és vegyes I/II. módú terhelések alatt kohéziós elemek használatával. Compos Struct 2014; 116: 509-22.
[7] Y Gong, B Zhang, L Zhao, J Zhang, N Hu, C Zhang. Vegyes módú I/II delamináció R-görbe viselkedése egy- és többirányú határfelületű szén/epoxi laminátumokban. Compos Struct 2019. (Bírálat alatt).
[8] L Peng, J Xu, J Zhang, L Zhao. Vegyes módú delamináció növekedése többirányú kompozit laminátumokban fárasztó terhelés alatt. Eng Fract Mech 2012; 96: 676-86.
[9] J Zhang, L Peng, L Zhao, B Fei. Kompozit laminátumok fáradásos delaminációjának növekedési ütemei és küszöbértékei vegyes módú terhelés alatt. Int J Fatigue 2012; 40: 7-15.
[10] Y Gong, L Zhao, J Zhang, Y Wang, N Hu. Delamináció terjedési kritérium, beleértve a szálak áthidalásának hatását vegyes módú I/II delamináció esetén CFRP többirányú laminátumokban. Compos Sci Technol 2017; 151: 302-9.
[11] Y Gong, B Zhang, SR Hallett. Delaminációs migráció többirányú kompozit laminátumokban I. módú kvázistatikus és fárasztó terhelés alatt. Compos Struct 2018; 189: 160-76.
[12] Y Gong, B Zhang, S Mukhopadhyay, SR Hallett. Kísérleti vizsgálat a delamináció migrációjáról többirányú laminátumokban II. módú statikus és fárasztó terhelés alatt, összehasonlítással az I. módúval. Compos Struct 2018; 201: 683-98.
[13] Y Gong, L Zhao, J Zhang, N Hu. Továbbfejlesztett hatványfüggvény-kritérium a delamináció terjedésére nagyméretű száláthidalás hatására kompozit többirányú laminátumokban. Compos Struct 2018; 184: 961-8.
[14] Y Gong, Y Hou, L Zhao, W Li, G Yang, J Zhang, N Hu. Új, háromlineáris kohéziós zóna modell a DCB laminátumok delaminációjának növekedésére száláthidalás hatására. Compos Struct 2019. (Beküldendő)
[15] L Zhao, J Zhi, J Zhang, Z Liu, N Hu. XFEM szimuláció a kompozit laminátumok delaminációjához. Composites Part A: Applied Science and Manufacturing 2016; 80: 61-71.
[16] Zhao Libin, Gong Yu, Zhang Jianyu. A szálerősítésű kompozit laminátumok rétegzett hőtágulási viselkedésével kapcsolatos kutatási eredmények. Journal of Aeronautical Sciences 2019: 1-28.
Forrás:Gong Yu, Wang Yana, Peng Lei, Zhao Libin, Zhang Jianyu. Tanulmány a fejlett szénszálerősítésű kompozit laminátumok rétegzett hőtágulási viselkedéséről [C]. Mechanika és Mérnöki Tudományok - Numerikus Számítás és Adatelemzés 2019 Akadémiai Konferencia. Kínai Mechanikai Társaság, Pekingi Mechanikai Társaság, 2019. keresztül ixueshu
Közzététel ideje: 2019. november 15.